Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 3см 4см. Найдите радиус круга, вписанного в треугольник
Объяснение:
Пусть один катет а, другой катет b. . По т. о биссектрисе треугольника
, тогда а= .
По т. Пифагора а²+b²=(3+4)² ,( )²+b²=49 ,
+b²=49 , 9b²+16b²=49*16 , b²= , b== 5,6 (см)
a= =4,2 cм
S=1/2*Р*r . Найдем площадь прямоугольного треугольника
S=1/2*5,6*4,2=1/2*23,52 (см²) . Найдем периметр Р=16,8 см. Тогда
1/2*23,52=1/2*16,8*r , r= 23,52/16,8 , r=1,4 см
===============================
Теорема о биссектрисе треугольника " Биссектриса треугольника делит противоположную сторону на два отрезка, длины которых относятся так же, как длины соответствующих сторон."
Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 3см 4см. Найдите радиус круга, вписанного в треугольник
Объяснение:
Пусть один катет а, другой катет b. . По т. о биссектрисе треугольника
По т. Пифагора а²+b²=(3+4)² ,(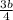
)²+b²=49 ,
a=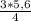
=4,2 cм
S=1/2*Р*r . Найдем площадь прямоугольного треугольника
S=1/2*5,6*4,2=1/2*23,52 (см²) . Найдем периметр Р=16,8 см. Тогда
1/2*23,52=1/2*16,8*r , r= 23,52/16,8 , r=1,4 см
===============================
Теорема о биссектрисе треугольника " Биссектриса треугольника делит противоположную сторону на два отрезка, длины которых относятся так же, как длины соответствующих сторон."
В условии ошибка: ВС ║AD, а не АС, так как параллельные прямые не могут проходить через одну точку.
BF = DE по условию,
∠AED = ∠CFB по условию,
∠CBF = ∠ADE как накрест лежащие при пересечении параллельных прямых ВС и AD секущей BD, ⇒
ΔCBF = ΔADE по стороне и двум прилежащим к ней углам.
Значит CF = AE,
BE = BF - EF, DF = DE - EF, а так как BF = DE, то и BE = DF,
∠CFD = ∠AEB как смежные с равными углами (∠AED = ∠CFB по условию),
значит ΔCFD = ΔAEB по двум сторонам и углу между ними.
Тогда ∠АВЕ = ∠CDF, а эти углы - накрест лежащие при пересечении прямых АВ и CD секущей BD, значит АВ║CD.