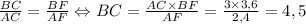1. 1)Треугольники АСЕ и АВД равны по второму признаку равенства треугольников.
Действительно, у них угол А - общий, АВ=АС по условию, углы АСЕ и АВД раны тоже по условию.
2) Т.к. в равных треугольниках соответственные стороны равны, то АЕ=АД=15 см, АС=АВ=7см, ЕС=ВД=10см
2. Треугольники АВС и А₁В₁С₁ равны по первому признаку равенства треугольников.
В них АВ=А₁В₁ по условию, АС = А₁С₁ по условию, ∠А=∠А₁ по условию.
В равных треугольниках соответственные углы В и В₁ равны.
Теперь рассмотрим треугольники АВК и А₁В₁К₁, они равны тоже по первому признаку, т.к. АВ=А₁В₁ по условию, углы В и В₁ равны по доказанному, а т.к. КС=К₁С₁ по условию и ВС=В₁С₁ по доказанному, то и остатки равных сторон ВК=В₁К₁
3. Треугольники АВС и А₁В₁С₁ равны по первому признаку, у них углы А и А₁ равны по условию, АВ=А₁В₁; АС=А₁С₁ по условию.
Значит, АС -ДС = А₁С₁-Д₁С₁, т.е. АД=А₁Д₁, как остатки равных сторон.
Тогда треугольники АВД и А₁В₁Д₁ равны по первому признаку равенства треугольников, в них АВ=А₁В₁ по условию, АД=А₁Д₁ по доказанному, ∠ А =∠ А₁
Она заключается в следующем: отношение сторон треугольника, содержащихся в угле, из которого проведена биссектриса, равна отношению отрезков, на которые делит биссектриса противолежащую сторону.
Назовем точку пересечения MN и биссектрисы AK через R; Тогда из данного в условии легко вывести, что биссектриса угла C проходит через R. Пусть RC ∩ AB = F; Пусть AM=2x, MB=x. Тогда x=2; По теореме Менелая для треугольника AMN: , ну а отсюда легко получить AF=2,4 и FM=1,6; Значит BF=3,6 и AF=2,4; По вышеизложенной теореме о биссектрисе имеем:
1. 1)Треугольники АСЕ и АВД равны по второму признаку равенства треугольников.
Действительно, у них угол А - общий, АВ=АС по условию, углы АСЕ и АВД раны тоже по условию.
2) Т.к. в равных треугольниках соответственные стороны равны, то АЕ=АД=15 см, АС=АВ=7см, ЕС=ВД=10см
2. Треугольники АВС и А₁В₁С₁ равны по первому признаку равенства треугольников.
В них АВ=А₁В₁ по условию, АС = А₁С₁ по условию, ∠А=∠А₁ по условию.
В равных треугольниках соответственные углы В и В₁ равны.
Теперь рассмотрим треугольники АВК и А₁В₁К₁, они равны тоже по первому признаку, т.к. АВ=А₁В₁ по условию, углы В и В₁ равны по доказанному, а т.к. КС=К₁С₁ по условию и ВС=В₁С₁ по доказанному, то и остатки равных сторон ВК=В₁К₁
3. Треугольники АВС и А₁В₁С₁ равны по первому признаку, у них углы А и А₁ равны по условию, АВ=А₁В₁; АС=А₁С₁ по условию.
Значит, АС -ДС = А₁С₁-Д₁С₁, т.е. АД=А₁Д₁, как остатки равных сторон.
Тогда треугольники АВД и А₁В₁Д₁ равны по первому признаку равенства треугольников, в них АВ=А₁В₁ по условию, АД=А₁Д₁ по доказанному, ∠ А =∠ А₁
равны по условию.
Будем пользоваться теоремой о биссектрисе.
Она заключается в следующем: отношение сторон треугольника, содержащихся в угле, из которого проведена биссектриса, равна отношению отрезков, на которые делит биссектриса противолежащую сторону.
Назовем точку пересечения MN и биссектрисы AK через R; Тогда из данного в условии легко вывести, что биссектриса угла C проходит через R. Пусть RC ∩ AB = F; Пусть AM=2x, MB=x. Тогда x=2; По теореме Менелая для треугольника AMN: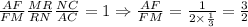
, ну а отсюда легко получить AF=2,4 и FM=1,6; Значит BF=3,6 и AF=2,4; По вышеизложенной теореме о биссектрисе имеем: 