Объяснение: Итак AC=7 и BD=6 - диагонали трапеции, AD= 8 и ВС=3 - основания трапеции. Проведем через С отрезок СК параллельный BD , где К- точка пересечения с прямой основаня AD. Имеем треугольник АСК со сторонами АС=7, СК=6, АК= 8+3=11.
DK=ВС=3, так как ABDK- параллелогамм по построению.
Заметим, что площадь треугольника АСК равна площади трапеции ABCD, т.к. треугольник ACD общий , а треугольники АВС и CDK имеют одинаковую площадь. ( ВС=DK - основания треугольников, а высота, проведенная к основанию у обоих треугольников есть высота трапеции ABCD, т.е. тоже равны)
Найдем площадь треугольника АСК по теореме Герона.
ответ: 6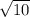
Объяснение: Итак AC=7 и BD=6 - диагонали трапеции, AD= 8 и ВС=3 - основания трапеции. Проведем через С отрезок СК параллельный BD , где К- точка пересечения с прямой основаня AD. Имеем треугольник АСК со сторонами АС=7, СК=6, АК= 8+3=11.
DK=ВС=3, так как ABDK- параллелогамм по построению.
Заметим, что площадь треугольника АСК равна площади трапеции ABCD, т.к. треугольник ACD общий , а треугольники АВС и CDK имеют одинаковую площадь. ( ВС=DK - основания треугольников, а высота, проведенная к основанию у обоих треугольников есть высота трапеции ABCD, т.е. тоже равны)
Найдем площадь треугольника АСК по теореме Герона.
Sack=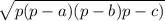 =
= 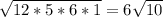
p= (7+6+11)/2=12
6√10 ед²
Объяснение: