в шаре радиуса 30см проведена секущая плоскость ,которая делит перпендикулярный ей диаметр в отношении 1:4.найдите площадь сечения шара этой плоскостью
гипотенуза делится на 2 отрезка: 10х и 3х (х длина одной части гипотенузы); 2) из одной вершины треугольника две касательные равные: 3х; из второй вершины две касательные равные: 10х; из третьей вершины две касательные равные: у; 3) гипотенуза равна 3х+10х=13х; один катет равен 3х+у; второй катет равен 10х+у; 4) радиус вписанной окружности в прямоугольный треугольник находится по формуле: r=(a+b-c)/2; 5)подставим наши значения: 4=(3х+у+10х+у-13х)/2; 2у=8; у=4; 5) значит, один катет равен 3х+4; второй катет равен 10х+4; по теореме Пифагора: (13х)^2=(3х+4)^2+(10х+4)^2; 169х^2=9х^2+24х+16+100х^2+80х+16; 15х^2-26х-8=0; х=2; х=-4/15 (отрицательный корень нам не нужен); 6) гипотенуза равна: 13х=13*2=26; один катет равен: 3х+4=3*2+4=10; второй катет равен: 10х+4=10*2+4=24; ответ: 10; 24; 26
Из точки А проведены две секущие АВ и АС, которые пересекают окружность в точках К и М так, что AB = 2 см, ВС = 4 см, AC = 5 см, AK = 1 см. Найдите МК.
Объяснение:
1)∠AKM =180°-∠BKM по т. о смежных углах ; ∠C=180°-∠BKM по свойству углов вписанного 4-х угольника ⇒ ∠AKM =∠C.
2) ΔAKM ~ΔACB по двум углам : ∠A_общий , ∠AKM =∠C.
Сходственные стороны в подобных треугольниках пропорциональны : , ⇒ MK=(1*4):5=0,8 (см)
============================
Свойство углов вписанного 4-х угольника
Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
гипотенуза делится на 2 отрезка: 10х и 3х (х длина одной части гипотенузы); 2) из одной вершины треугольника две касательные равные: 3х; из второй вершины две касательные равные: 10х; из третьей вершины две касательные равные: у; 3) гипотенуза равна 3х+10х=13х; один катет равен 3х+у; второй катет равен 10х+у; 4) радиус вписанной окружности в прямоугольный треугольник находится по формуле: r=(a+b-c)/2; 5)подставим наши значения: 4=(3х+у+10х+у-13х)/2; 2у=8; у=4; 5) значит, один катет равен 3х+4; второй катет равен 10х+4; по теореме Пифагора: (13х)^2=(3х+4)^2+(10х+4)^2; 169х^2=9х^2+24х+16+100х^2+80х+16; 15х^2-26х-8=0; х=2; х=-4/15 (отрицательный корень нам не нужен); 6) гипотенуза равна: 13х=13*2=26; один катет равен: 3х+4=3*2+4=10; второй катет равен: 10х+4=10*2+4=24; ответ: 10; 24; 26
Из точки А проведены две секущие АВ и АС, которые пересекают окружность в точках К и М так, что AB = 2 см, ВС = 4 см, AC = 5 см, AK = 1 см. Найдите МК.
Объяснение:
1)∠AKM =180°-∠BKM по т. о смежных углах ; ∠C=180°-∠BKM по свойству углов вписанного 4-х угольника ⇒ ∠AKM =∠C.
2) ΔAKM ~ΔACB по двум углам : ∠A_общий , ∠AKM =∠C.
Сходственные стороны в подобных треугольниках пропорциональны :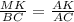 ,
,  ⇒ MK=(1*4):5=0,8 (см)
⇒ MK=(1*4):5=0,8 (см)
============================
Свойство углов вписанного 4-х угольника
Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.