В правильной шестиугольной призме АВСТЕНA1B1C1T1E1H1 с высотой 2 и стороной основания 1 точка M – середина ребра СС1. Найдите угол между прямой AM и плоскостью ВВ1С1.
По условию, вd=11.3 см, и он является катетом в прямоуг. треугольнике bdc. гипотенуза этого треугольника (bd) в 2 раза меньше катета=> по свойству прямоугольного треугольника если катет в 2 раза меньше гипотенузы то острый угол напротив этого катета равен 30 градусам. то есть > с равен 30 градусам. так как авс равнобедренный, углы при основании равны то есть < а=< с=30 градусов. мы знаем, что сумма углов треугольника равна 180. тогда < а=180-30-30=120 градусов. ответ: < вас=30 < вса=30 < авс=120
Для любой правильной призмы справедливы формулы:
Площадь боковой поверхности:
Sбок = Pосн · h, где
Росн - периметр основания,
h - высота.
Площадь полной поверхности:
Sполн = Sбок + 2Sосн
Объем:
V = Sосн · h
____________________
a - сторона основания.
____________________
Правильная треугольная призма:
в основании лежит правильный треугольник, значит
Sосн =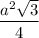
Sбок = 3а · h
Sполн = 3a · h + 2 · a²√3/4 = 3ah + a²√3/2
____________________
Правильная четырехугольная призма:
в основании - квадрат, значит
Sосн = a²
Sбок = 4ah
Sполн = 4ah + 2a²
V = a²h
____________________
Правильная шестиугольная призма:
Sосн =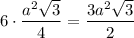
Sбок = 6ah
Sполн = 6ah + 2 · 3a²√3/2 = 6ah + 3a²√3