Здесь даже чертеж не нужен (хотя он для наглядности приложен)
Помним теорему синусов треугольника:
Где угол лежит напротив стороны , угол лежит напротив стороны , а угол лежит напротив стороны , а - радиус описанной около треугольника окружности (правда, окружность в этой задаче нам не нужна)
Учитывая, что
Но тогда теорему синусов можно переписать так:
Что и требовалось доказать.
Можно ещё по-другому пойти.
Смотрим на рисунок. (нижние углы), то есть треугольник равнобедренный с основанием , значит, боковые стороны равны, то есть
Далее, , то треугольник равнобедренный с основанием , боковые стороны равны, то есть
PΔ=36, треугольник правильный, значит сторона треугольника равна : 36:3=12. Опустим высоту в треугольнике до пересечения с окружностью. Соединим полученную точку с одной из оставших вершин заданного треугольника. Получим прямоугольный треугольник, гипотенуза которого является диаметром окружности. Угол между высотой треугольника и его стороной равен 30°. Высота в правильном треугольнике является и биссектрисой и медианой. 60°:2=30°. Вычислим диаметр окружности: d=12:cos30°=12:(√3/2)=24/√3=24·√3/√3·√3=24√3/3=8√3. Диагональю квадрата является диаметр окружности. Обозачим сторону квадрата через а. По теореме Пифагора: a²+a²=d², 2a²=(8√3)². 2a²=64·3, a²=32·3=16·2·3, a=√16·6=4√6. a=4√6.
Здесь даже чертеж не нужен (хотя он для наглядности приложен)
Помним теорему синусов треугольника:
Где угол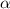 лежит напротив стороны
лежит напротив стороны  , угол
, угол 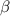 лежит напротив стороны
лежит напротив стороны 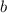 , а угол
, а угол 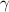 лежит напротив стороны
лежит напротив стороны  , а
, а 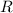 - радиус описанной около треугольника окружности (правда, окружность в этой задаче нам не нужна)
- радиус описанной около треугольника окружности (правда, окружность в этой задаче нам не нужна)
Учитывая, что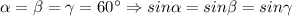
Но тогда теорему синусов можно переписать так:
Что и требовалось доказать.
Можно ещё по-другому пойти.
Смотрим на рисунок.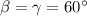 (нижние углы), то есть треугольник равнобедренный с основанием
(нижние углы), то есть треугольник равнобедренный с основанием  , значит, боковые стороны равны, то есть
, значит, боковые стороны равны, то есть 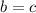
Далее,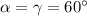 , то треугольник равнобедренный с основанием
, то треугольник равнобедренный с основанием 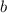 , боковые стороны равны, то есть
, боковые стороны равны, то есть 
Ну и завершающий вывод:
Что и требовалось доказать.
36:3=12.
Опустим высоту в треугольнике до пересечения с окружностью. Соединим полученную точку с одной из оставших вершин заданного треугольника. Получим прямоугольный треугольник, гипотенуза которого является диаметром окружности. Угол между высотой треугольника и его стороной равен 30°. Высота в правильном треугольнике является и биссектрисой и медианой. 60°:2=30°.
Вычислим диаметр окружности:
d=12:cos30°=12:(√3/2)=24/√3=24·√3/√3·√3=24√3/3=8√3.
Диагональю квадрата является диаметр окружности. Обозачим сторону квадрата через а.
По теореме Пифагора: a²+a²=d², 2a²=(8√3)².
2a²=64·3,
a²=32·3=16·2·3,
a=√16·6=4√6.
a=4√6.