¤
¤
¤
в параллелограмме abcd угол d равен 120°. высота вн делит сторону ad на две равные части. найдите длину диагонали вd, если периметр параллелограмма равен 24 см.​

11.

Дано:

ΔАВС - равнобедренный

АС = ВС = 13

АВ = 10

Найти:

АС - высоту. опущенную на боковую сторону

СD - высота равнобедренного треугольника. опущенная на основание, является и медианой. Поэтому AD = BD = 0.5AB = 0.5 · 10 = 5.

По теореме Пифагора

АС² = CD² + AD²

13² = CD² + 5²

CD² = 13² - 5² = 144 = 12²

CD = 12

Площадь треугольника АВС

S = 0.5 CD · AB = 0.5 · 12 · 10 = 60

Площадь треугольника АВС можно также вычислить и так:

S = 0.5 BC · AE

откуда

АЕ = 2S : BC = 2 · 60 : 13 = 9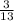 ≈ 9.23

АЕ = 9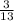 ≈ 9.23

12.

Дано:

MKNR - ромб

KR = 10 - 1-я диагональ ромба

MN = 12 - 2-я диагональ ромба

Найти:

МК - сторону ромба

Пусть О - точка пересечения диагоналей ромба.

Диагонали ромба делятся точкой пересечения пополам, поэтому

КО = 0,5 KR = 0.5 · 10 = 5

МО = 0,5 MN = 0.5 · 12 = 6

Диагонали ромба пересекаются под прямым углом, поэтому

КО ⊥ МО и ΔМКО - прямоугольный с гипотенузой МК.

По теореме Пифагора

МК² = КО² + МО²

МК² = 5² + 6² = 61

МК = √61 ≈ 7,81

Сторона ромба МК =√61 ≈ 7,81

Не верное утверждение Г.

Объяснение:

А) Прямоугольные треугольники с соответственно равными острыми углами (а даже и с одним, так как второй - прямой) ПОДОБНЫ. Отношение площадей подобных фигур равно квадрату коэффициента подобия (отношению линейных размеров). Значит отношение гипотенуз равно √(2/3). Утверждение верное.

Б) Диагональ трапеции делит ее на два треугольника с одинаковой высотой, следовательно их площади относятся, как их основания, к которым проведена эта высота. Утверждение верное.

В). Медиана треугольника делит треугольник на два треугольника, у которых равны и основания, и высоты. Значит и их площади равны. Утверждение верное.

Г). Периметры равновеликих треугольников в общем случае НЕ равны. (Предыдущий пример с медианой, когда треугольник не равнобедренный - периметры разные). Утверждение НЕ верное.