Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то треугольники подобны.
Дано: ∠А = ∠А₁; АВ : А₁В₁ = АС : А₁С₁ . Доказать: ΔАВС подобен ΔА₁В₁С₁. Доказательство: Достроим на стороне АС треугольник АВ₂С, в котором углы, прилежащие к стороне АС, равны углам в треугольнике А₁В₁С₁ (как на рисунке) . Тогда ΔАВ₂С подобен ΔА₁В₁С₁ по двум углам. Запишем отношение сторон в этих треугольниках: АВ₂ : А₁В₁ = АС : А₁С₁. Сравним полученную пропорцию с данной в условии: АВ : А₁В₁ = АС : А₁С₁ Значит, АВ₂ = АВ. Но тогда ΔАВС = ΔАВ₂С по двум сторона и углу между ними (АС - общая, АВ₂ = АВ и ∠А = ∠А₁ = ∠1 по условию). Итак, ΔАВС = ΔАВ₂С, а ΔАВ₂С подобен ΔА₁В₁С₁, значит ΔАВС подобен ΔА₁В₁С₁. Доказано.
Боковые стороны трапеции ABCD равны соответственно 20 и 25, а верхнее основание равно 5. Биссектриса угла проходит через середину боковой стороны в 20 ед.. Найдите площадь трапеции.
2) Проведем МК║АD ⇒ РМ-средняя линия , АР=РВ=12,5 .
Тогда ∠DАМ=∠РМА как накрест лежащие , при АМ-секущей и ∠РАМ=∠DАМ ⇒ ∠РАМ=∠РМD ⇒ ΔАМР- равнобедренный и АР=РМ=12,5.
3) По т. о средней линии трапеции РМ= , 12,5= ,AD=20 .
4) Проведем СК║АВ , тогда АВСК-параллелограмм и СК=25.
Рассмотрим ΔКСD. Проверим т. обратную т. Пифагора :
25²=625 ; 15²+20²=225+400=625 , а 625=625 ⇒ΔКСD-прямоугольный и CD⊥AD ( см чертеж 2). Поэтому боковая сторона СD -высота.
5) S (трапеции) =1/2*h*(a+b) ; S (трапеции) =1/2*20*(20+5) =50 (ед²)
=============================
Теорема ,обратная т. Пифагора : Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник является прямоугольным.
Дано: ∠А = ∠А₁; АВ : А₁В₁ = АС : А₁С₁ .
Доказать: ΔАВС подобен ΔА₁В₁С₁.
Доказательство:
Достроим на стороне АС треугольник АВ₂С, в котором углы, прилежащие к стороне АС, равны углам в треугольнике А₁В₁С₁ (как на рисунке) .
Тогда ΔАВ₂С подобен ΔА₁В₁С₁ по двум углам. Запишем отношение сторон в этих треугольниках:
АВ₂ : А₁В₁ = АС : А₁С₁.
Сравним полученную пропорцию с данной в условии:
АВ : А₁В₁ = АС : А₁С₁
Значит, АВ₂ = АВ.
Но тогда ΔАВС = ΔАВ₂С по двум сторона и углу между ними (АС - общая, АВ₂ = АВ и ∠А = ∠А₁ = ∠1 по условию).
Итак, ΔАВС = ΔАВ₂С, а ΔАВ₂С подобен ΔА₁В₁С₁, значит
ΔАВС подобен ΔА₁В₁С₁.
Доказано.
Боковые стороны трапеции ABCD равны соответственно 20 и 25, а верхнее основание равно 5. Биссектриса угла проходит через середину боковой стороны в 20 ед.. Найдите площадь трапеции.
Объяснение:
1) Пусть АВСD-трапеция, АВ=25 , ВС=5 ,СD=20 , АМ-биссектриса.
2) Проведем МК║АD ⇒ РМ-средняя линия , АР=РВ=12,5 .
Тогда ∠DАМ=∠РМА как накрест лежащие , при АМ-секущей и ∠РАМ=∠DАМ ⇒ ∠РАМ=∠РМD ⇒ ΔАМР- равнобедренный и АР=РМ=12,5.
3) По т. о средней линии трапеции РМ=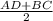
, 12,5=
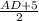,AD=20 .
4) Проведем СК║АВ , тогда АВСК-параллелограмм и СК=25.
Рассмотрим ΔКСD. Проверим т. обратную т. Пифагора :
25²=625 ; 15²+20²=225+400=625 , а 625=625 ⇒ΔКСD-прямоугольный и CD⊥AD ( см чертеж 2). Поэтому боковая сторона СD -высота.
5) S (трапеции) =1/2*h*(a+b) ; S (трапеции) =1/2*20*(20+5) =50 (ед²)
=============================
Теорема ,обратная т. Пифагора : Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник является прямоугольным.