Угол Е = 180-120=60°( как смежные углы,сумма смежных углов 180°). сумма острых углов равна 90°
угол С= 90-60=30°. катет, который лежит напротив угла равного 30° равен 1/2 гипотезы. CD= 2*7=17 см
2
сумма острых углов прямоугольного треугольника 90°. Пусть один угол х, другой х+6
х+х+6=90
2х= 84
х= 42° первый угол
42+6=48° второй угол.
3
у ранобедренрог треугольника углы при основании равны.
Рассмотрим треугольники КАО и РВО. КА=РВ, КО=РО по условию. угол К=уголу Р. значит треугольники КАО и РВО равные по первому признаку ( двум сторонам и углу между ними). Отсюда следует что все соответствующие элементы равны. ОА=ОВ
Обратная теорема Фалеса: Если две или более прямых отсекают от двух других прямых равные или пропорциональные отрезки, то они параллельные. Утверждение справедливо, независимо от того, параллельные прямые или пересекаются.
⇒ ЕК || ОМ || АС
2. Рассмотрим АВС.
АЕ = ЕВ; СК = КВ (АК и СЕ - медианы)
⇒ ЕК - средняя линия (по определению)
Средняя линия равна половине основания.
⇒
3. Рассмотрим ΔАЕК.
АО = ОК; ОН || ЕК.
Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок - средняя линия этого треугольника.
Объяснение:
1
Угол Е = 180-120=60°( как смежные углы,сумма смежных углов 180°). сумма острых углов равна 90°
угол С= 90-60=30°. катет, который лежит напротив угла равного 30° равен 1/2 гипотезы. CD= 2*7=17 см
2
сумма острых углов прямоугольного треугольника 90°. Пусть один угол х, другой х+6
х+х+6=90
2х= 84
х= 42° первый угол
42+6=48° второй угол.
3
у ранобедренрог треугольника углы при основании равны.
Рассмотрим треугольники КАО и РВО. КА=РВ, КО=РО по условию. угол К=уголу Р. значит треугольники КАО и РВО равные по первому признаку ( двум сторонам и углу между ними). Отсюда следует что все соответствующие элементы равны. ОА=ОВ
Объяснение:
Дано: ΔАВС;
АК и СЕ - медианы;
СМ = МЕ; АО = ОК;
АС = а
Найти: ОМ.
1. СМ = МЕ; АО = ОК
Обратная теорема Фалеса: Если две или более прямых отсекают от двух других прямых равные или пропорциональные отрезки, то они параллельные. Утверждение справедливо, независимо от того, параллельные прямые или пересекаются.⇒ ЕК || ОМ || АС
2. Рассмотрим АВС.
АЕ = ЕВ; СК = КВ (АК и СЕ - медианы)
⇒ ЕК - средняя линия (по определению)
Средняя линия равна половине основания.⇒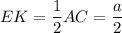
3. Рассмотрим ΔАЕК.
АО = ОК; ОН || ЕК.
Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок - средняя линия этого треугольника.⇒ ОН - средняя линия ΔАЕК.
4. Рассмотрим ΔЕКС.
СМ = МЕ; МР || ЕК;
⇒МР - средняя линия ΔЕКС.
5. Рассмотрим ΔАЕС.
АН = НЕ (п.3); НМ || AC
⇒ НМ - средняя линия ΔАЕС.
6. Рассмотрим ΔАКС.
КР = РС (п.4); ОР || АС;
⇒ ОР - средняя линия ΔАКС.
7.