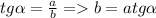Если у прямоугольных треугольников равен острый угол, то это значит, что тангенс этого угла будет одинаковый у обоих треугольников. Тангенс - это отношение противолежащего катета к прилежащему. Значит,
- равный угол, а и b - катеты. Из выражения видим, что если тангенс и один из катетов у треугольников равны, то и второй катет у них тоже будет равным. Если у прямоугольных треуцгольников равны 2 катета, то корень и суммы их квадратов(это их гипотенуза) у них тоже будет равным. Или же они равны по двум катетам и углу между ними.
Вопрос не совсем понятен, но определим длины векторов:
Модуль вектора |ab|=√[(Xb-Xa)²+(Yb-Ya)²] или |ab|=√[(-2+4)²+(4-1)²]=√13.
Модуль вектора |bc|=√[(Xc-Xb)²+(Yc-Yb)²] или bc|=√[(2+2)²+(5-4)²]=√17.
Модуль вектора |cd|=√[(Xd-Xc)²+(Yd-Yc)²] или |cd|=√[(0-2)²+(2-5)²]=√13.
Модуль вектора |ad|=√[(Xd-Xa)²+(Yd-Ya)²] или |ad|=√[(0+4)²+(2-1)²]=√17.
Модуль вектора |ac|=√[(Xc-Xa)²+(Yc-Ya)²] или |ac|=√[(2+4)²+(5-1)²]=√52.
Модуль вектора |bd|=√[(Xd-Xb)²+(Yd-Yb)²] или |bd|=√[(0+2)²+(2-4)²]=√8.
Верные равенства:
Равны МОДУЛИ векторов |AB|=|CD| и |BC|=|AD|,
а так как равные вектора это сонаправленные вектора, с равными модулями, то
равны вектора АВ=DС, BA=CD, CB=DA и BC=AD.
Что и требовалось доказать
Объяснение:
Если у прямоугольных треугольников равен острый угол, то это значит, что тангенс этого угла будет одинаковый у обоих треугольников. Тангенс - это отношение противолежащего катета к прилежащему. Значит,