Меньшее основание равнобедренной трапеции равно 10 см. Точка пересечения диагоналей отдалена от оснований на 2 см и 3 см. Найдите площадь этой трапеции.
Чертёж смотрите во вложении.
Дано:
Четырёхугольник ABCD - равнобедренная трапеция (AD = BC, DC и АВ - основания).
DC < АВ.
АС и DB - диагонали.
Точка О - точка пересечения АС и DB.
ОЕ - расстояние от точки О до DC.
ОН - расстояние от точки АВ.
ОЕ = 2 см.
ОН = 3 см.
DC = 10 см.
Найти:
S(ABCD) = ?
Рассмотрим ΔDOC и ΔBOA. По свойству трапеции ΔDOC ~ ΔBOA (это не сложно доказать, если рассмотреть пару равных накрест лежащих углов при параллельных прямых).
ОН - высота ΔBOA, ОЕ - высота ΔDOC. У подобных треугольников отношение линейных элементов (медиан, биссектрис, высот и так далее) равно коэффициенту подобия.
∠DOC = ∠AOB (так как они вертикальные). В подобных треугольниках против равных углов лежат сходственные стороны. А отношение сходственных сторон подобных треугольников равно коэффициенту подобия.
То есть -
Подставим известные нам значения в формулу -
AB = 15 см.
Площадь трапеции равна произведению полусуммы оснований и высоты оснований.
Отрезок ЕН - высота, так как перпендикулярна основаниям. ЕН = ОЕ+ОН = 2 см+3 см = 5 см.
Полусумма оснований = 0,5*(DC+АВ) = 0,5*(10 см+15 см) = 0,5*25 см = 12,5 см.
Меньшее основание равнобедренной трапеции равно 10 см. Точка пересечения диагоналей отдалена от оснований на 2 см и 3 см. Найдите площадь этой трапеции.
Чертёж смотрите во вложении.
Дано:
Четырёхугольник ABCD - равнобедренная трапеция (AD = BC, DC и АВ - основания).
DC < АВ.
АС и DB - диагонали.
Точка О - точка пересечения АС и DB.
ОЕ - расстояние от точки О до DC.
ОН - расстояние от точки АВ.
ОЕ = 2 см.
ОН = 3 см.
DC = 10 см.
Найти:
S(ABCD) = ?
Рассмотрим ΔDOC и ΔBOA. По свойству трапеции ΔDOC ~ ΔBOA (это не сложно доказать, если рассмотреть пару равных накрест лежащих углов при параллельных прямых).
ОН - высота ΔBOA, ОЕ - высота ΔDOC. У подобных треугольников отношение линейных элементов (медиан, биссектрис, высот и так далее) равно коэффициенту подобия.
∠DOC = ∠AOB (так как они вертикальные). В подобных треугольниках против равных углов лежат сходственные стороны. А отношение сходственных сторон подобных треугольников равно коэффициенту подобия.
То есть -
Подставим известные нам значения в формулу -
AB = 15 см.
Площадь трапеции равна произведению полусуммы оснований и высоты оснований.
Отрезок ЕН - высота, так как перпендикулярна основаниям. ЕН = ОЕ+ОН = 2 см+3 см = 5 см.
Полусумма оснований = 0,5*(DC+АВ) = 0,5*(10 см+15 см) = 0,5*25 см = 12,5 см.
S(ABCD) = 12,5 см*5 см = 62,5 см².
ответ: 62,5 см².
ответ: КК1 = 12 см
Объяснение: Исправим условие
Отрезок MN не пересекает плоскость а. Точка К принадлежит
отрезку MN. Через точки M, и N проведены параллельные
прямые, пересекающие плоскость а в точках М1, K1, и N 1
соответственно. Найдите длину отрезка КК1, если MM1 = 6 см,
NN1 = 21 см и МК: KN = 2:3.
Теперь решим.
Для начала проведем параллельно плоскости прямую МН. тогда Поучится треугольник MNH сторона NH которого 6 см,
а МК:КN = 2:3. Треугольники МКЕ и МNH подобные, так как угол М общий, а углы МКЕ и MNH равны как соответственные.
Тогда MN = 5х, а МК = 2х
МН:КЕ = 5х:2х=5:2, значит КЕ =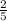 МН =
МН = 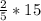 = 6 с м
= 6 с м
Итак, отрезок КЕ = 6 см
КК1 = КЕ+ЕК1 = 6+6=12 см
КК1 = 12 см