У циліндрі паралельно його осі проведено площину, що перетинає основу по хорді, яку видно із центра цієї основи під кутом 120°. Площа перерізу, що при цьому утворився, дорівнює 36√6 см², а кут нахилу діагоналі перерізу до площини основи дорівнює 30°. Знайдіть площу повної поверхні циліндра.

Показать ответ

Ответ:

ibarabol318

05.05.2023 06:05

Правильное условие:

В треугольнике ABC AB=√21, BC=3√21. Биссектриса внешнего угла треугольника при вершине B пересекает прямую AC в точке P, угол APB равен 30°. Найдите BP.

Внешний угол треугольника равен сумме двух других не смежных с ним.

Пусть ∠CAB = y; ∠BCA = x.

Тогда внешний угол при вершине B равен x+y.

Биссектриса делит угол пополам, поэтому ∠ABP =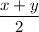 $\dfrac{x+y}2$

По свойству внешнего угла из ΔAPB имеем:

∠CAB = ∠APB+∠ABP;

y = 30°+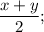 $\dfrac{x+y}2;$

2y = 60°+x+y;

y = 60°+x = ∠CAB.

В ΔABC, по теореме синусов, получим равенство:

$\dfrac{BC}{\sin\left( \angle CAB\right) } =\dfrac{AB}{\sin\left( \angle BCA\right) };\\\\BC\cdot \sin\left( \angle BCA\right) =AB\cdot \sin\left( \angle CAB\right) ;$

3√(21)·sin(x) = √(21)·sin(60°+x);

3sin(x) = sin(60°)·cos(x)+cos(60°)·sin(x);

3sin(x) =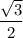 $\dfrac{\sqrt3}2$ ·cos(x)+ $\dfrac12$ ·sin(x);

6sin(x)-sin(x) = 5sin(x) = √(3)·cos(x);

Если cos x = 0, то sin x = 0, но синус и косинус не могут одновременно равняться нулю, тогда поделим на cos x ≠ 0;

tg(x) =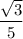 $\dfrac{\sqrt3}5$ .

Найдём sin(x):

${\tt tg}^2x=\dfrac1{\cos ^2x}-1\Leftrightarrow \cos ^2x=\dfrac1{{\tt tg}^2x+1};\\\\\cos^2x=\dfrac1{\dfrac3{25}+1} =\dfrac{25}{3+25} =\dfrac{25}{28};$

По основному тригонометрическому тождеству:

$\sin ^2x=1-\cos^2x=1-\dfrac{25}{28} =\dfrac{28-25}{28} =\dfrac3{28};$

sin(x) = +√(3/28) т.к. 0 < x < 180°, как угол треугольника.

По теореме синусов в ΔCPB:

$\dfrac{BP}{\sin \left( \angle BCA\right) }=\dfrac{BC}{\sin \left( \angle CPB\right) };\\\\BP=\dfrac{BC\cdot \sin \left( \angle BCA\right) }{\sin \left( \angle CPB\right) };\\\\BP=\dfrac{3\sqrt{21}\cdot \sin x}{\sin 30^{\circ }} =\dfrac{3\sqrt{21}\cdot \dfrac{\sqrt3}{\sqrt{28}}}{1/2};\\\\BP=\dfrac{2\cdot 3\sqrt{21} \cdot \sqrt3}{2\sqrt7} =3\cdot (\sqrt3)^2=9$

ответ: 9.

Втреугольнике abc ab=21−−√, bc=321−−√, биссектриса внешнего угла при вершине b пересекает прямую ac

0,0(0 оценок)

Ответ:

лолкек64

13.03.2021 08:57

1) Периметр ΔАВО равен АВ+ВО+АО=8, но ВО =3⇒АО+АВ=8-3=5

Периметр ΔАВС равен АВ+ВС+АС=2АВ+2АО=2*(АВ+АО)=2*5=10/см/, т.к. ΔАВС - равнобедренный, это следует из того, что ВО- медиана и высота, проведенная к АС.

ответ 10 см.

2) Из ΔОКС (∠К=90°) по теореме Пифагора СО=√(4²+3²)=√25=5

Т.к. в ΔВОC OF - медиана и высота по условию, то ΔВОС - равнобедренный, т.е. ВО=СО=5

ответ ВО=5

3) Пусть ОК⊥АВ, К∈АВ, тогда КВ=0.5АВ=√(10²-6²)=√(100-36)=√64=8

SΔ AOB=AB*OK/2=6*8/2=24

В ΔВОС ОВ=СО, т.к. высота, проведенная из точки О, является и медианой, делит сторону ВС пополам, поэтому ОВ=ОС=10, обозначим М-основание высоты, проведенной к АС, тогда площадь ΔАОС равна ОМ*МС=5МС, МС найдем из ΔМОС,

МС=√(СО²-ОМ²)=√(100-25)=√75=5√√3, и SΔАОС=ОМ*МС=5МС=5*5√3=25√3

ответ 24 ед.кв., 25√3 ед. кв.

0,0(0 оценок)

Популярные вопросы: Геометрия