1) Пусть РО - расстояние от точки Р до плоскости (т.О ∈ плоскости, РО - высота пирамиды). Поскольку точка P находится на расстоянии 25 см от всех сторон треугольника, то т. О - центр круга, впис. в треугольник (r).
р=(20+34+42)/2=48
по формуле Герона S = = cм²
r=S/p, r=336/48= 7 см
За т. Пифагора ==24 см
2) Поскольку т. S находится на одинаковом расстоянии от вершин треугольника, то т.О - центр круга, опис. навк.треугольника.
Далее аналогично: найти р = 42 , потом S по формуле Герона (S = 210), а потом найти R = 39*28*17/4*210=22,1
угол1 + угол2= 180°-90°=90°
Найдем одну часть: 90°/3= 30°
угол1= 1 часть= 30°
угол2= 2 части= 30°*2= 60°
ответ: угол1=30°; угол2=60°
б)Треугольник равнобедренный, значит угол2= 70°
угол1= 180°-70°-70°= 40°
ответ: угол1=40°; угол2=70°
в)Треугольник прямоугольный, равнобедренный, значит
угол1+угол2=90°
В то же время угол1=угол2=> = 90°/2= 45°
ответ: угол1=45°; угол2=45°
г)угол3= 180°-150°=30°
угол1 + угол2= 180°-30°= 150°
угол2 - угол1= 10°=> угол2= 80°; угол1=70°
ответ: угол1=70°; угол2=80°
д)угол3= 180°-110°= 70°
Тругольник равнобедренный, значит угол1= угол3= 70°
угол2=180°-70°-70°= 40°
ответ: угол1=70°; угол 2=40°
е)угол3= 180°-40°= 140°
угол1 + угол2= 180°-140°= 40°
угол1+угол2= 8 частей( из отношения 5:3)=>
1 часть равна 40°/8= 5°
угол1= 5°*5= 25°
угол2= 5°*3= 15°
ответ: угол1=25°; угол2=15°
24 см
Объяснение:
1) Пусть РО - расстояние от точки Р до плоскости (т.О ∈ плоскости, РО - высота пирамиды). Поскольку точка P находится на расстоянии 25 см от всех сторон треугольника, то т. О - центр круга, впис. в треугольник (r).
р=(20+34+42)/2=48
по формуле Герона S =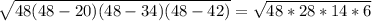
=
cм²
r=S/p, r=336/48= 7 см
За т. Пифагора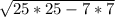
=
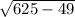=24 см
2) Поскольку т. S находится на одинаковом расстоянии от вершин треугольника, то т.О - центр круга, опис. навк.треугольника.
Далее аналогично: найти р = 42 , потом S по формуле Герона (S = 210), а потом найти R = 39*28*17/4*210=22,1
Далее использовать т. Пифагора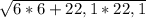
=22,9