Точка пересечения O — серединная точка для обоих отрезков PG и RS.
Найди величину сторон PR и RO в треугольнике PRO, если GS=32,7 см и SO=41,7 см
(при ответе упорядочи вершины таким образом, чтобы углы при них были попарно равны)

А. так как отрезки делятся пополам, то
1) сторона RO в треугольнике PRO равна стороне (...) в треугольнике GSO;
2) сторона PO в треугольнике PRO равна стороне (...) в треугольнике
GSO
угол ROP равен углу (...) как вертикальный угол

Треугольники равны по первому признаку равенства треугольников.
В равных треугольниках соответствующие углы равны
PR= ...
RO= ...​

Извини уж, под рукой ни листа бумаги, ни карандаша нет, так что решу только задачи в которых есть рисунок.

1) Угол 1 и 2 равны. Т.е. Угол 2 равен 135 градусам.

3) Угол Р равен 180 градусов(сумма всех углов любого треугольника) минус угол О 60 и угол N 90. 180-60-90 = 30 градусов равен угол Р.

В прямоугольном треугольнике катет лежащий напротив угла 30 градусов, равен половине гипотенузы, значит катет ON равен 8/2=4.

Далее по теоеме Пифагора найдем другой катет. PN^2=PO^2-ON^2

PN^2=64-16=48. Значит PN =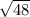 или 4

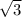
8) Треугольники PQH и QRH - прямоугольные, значит их площадь равна половине площади прямоугольника, со сторонами, равными катетам этих треугольников.

Площадь треугольника PQH = 9*12/2=54 Площадь треугольника QRH=12*16/2= 96.

Нужно найти площадь треугольника PQR= 54+96=150. ОТвет 150.

10) ML - средняя линия трапеции. Ее можно найти, посчитав полусумму оснований трапеции. Т.е. (BC+AD)/2.

ML=(7+15)/2=11. ответ 11.

Объяснение:

Расстояние от точки до прямой находится на перпендикуляре к прямой)))
основания трапеции параллельны, т.е. для них перпендикуляр общий...
этот перпендикуляр будет состоять из двух высот для треугольников,
опирающихся на основания трапеции...
одно основание меньше, другое больше --- это дано)))
треугольники, опирающиеся на основания трапеции подобны --- у них
равные углы (вертикальный и накрест лежащие при параллельных основаниях трапеции)))
следовательно, существует коэффициент подобия,
равный отношению сторон, в том числе и оснований трапеции...
k = a / b, a < b ---> k ≠ 1
этот же коэффициент связывает и высоты подобных треугольников,
и получим, что в меньшем треугольнике и высота меньше)))
ЧиТД