∠2 & ∠1 — накрест лежащие углы, и так как они друг другу равны, то BC ║AD.
Но это ещё не означает, что наш четырёхугольник — параллелограмм, всего лишь то противоположные друг другу пары прямых — параллельны.
Но у нас есть ещё одно условие: BC == AD. А вот это уже означает, что четырёхугольник — параллелограмм, так как каждые противолежащие друг другу пары сторон во первых: друг другу параллельны.
Во вторых: равны.
6. Так как ΔABC == ΔCDA, то AD == BC, BA == DC, ∠B == ∠D => ∠A == ∠C.
А по 2-ому признаку параллелограмма: все противоположные углы попарно равны, что и означает, что четырёхугольник ABCD — параллелограмм.
Т. косинусов "Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними"
5.
У нас есть данные: ∠2 == ∠1.
∠2 & ∠1 — накрест лежащие углы, и так как они друг другу равны, то BC ║AD.
Но это ещё не означает, что наш четырёхугольник — параллелограмм, всего лишь то противоположные друг другу пары прямых — параллельны.
Но у нас есть ещё одно условие: BC == AD. А вот это уже означает, что четырёхугольник — параллелограмм, так как каждые противолежащие друг другу пары сторон во первых: друг другу параллельны.
Во вторых: равны.
6. Так как ΔABC == ΔCDA, то AD == BC, BA == DC, ∠B == ∠D => ∠A == ∠C.
А по 2-ому признаку параллелограмма: все противоположные углы попарно равны, что и означает, что четырёхугольник ABCD — параллелограмм.
Найдите периметр треугольника с площадью 10√3 см² и углом 60°, если стороны, прилежащие к данному углу, относятся как 5:8.
Объяснение:
Пусть в ΔАВС , ∠В=60° , АВ:ВС=5:8.
Если одна часть х см , то АВ=5х, ВС=8х.
S( треуг.) = 1/2*АВ*ВС*sinВ или 10√3=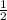 *5х*8х*
*5х*8х*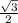 , х²=1 , х=1 ⇒
, х²=1 , х=1 ⇒
АВ=5 см , ВС=8 см .
По т. косинусов АС²=АВ²+ВС²-2*АВ*ВС*cosВ,
АС²=25+64-2*5*8*cos60, АС²=89-2*5*8*1/2, АС=7 см
Р=5+8+7=20 ( см)
====================
S( треуг.) = 1/2*а*в* sinα
Т. косинусов "Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними"