Точка h является точкой пересечения высот aa1 и bb1 остроугольного треугольника abc. продолжение высоты bb1 за точку b1 пересекает окружность, описанную около треугольника abc в точке b2. известно, что ah=ah1, bh=b2h. найти угол acb
Чтобы найти координаты вектора, нужно от координат конца отнять соответствующие координаты начала. Очевидно, что при смене местами начала и конца вектора, например ВС, у нового, в этом случае СВ, соответвующие координаты будут равны по модулю и противоположны по знаку.
AB и DC, BA и CD, AD и BC, DA и CB
Объяснение:
Чтобы найти координаты вектора, нужно от координат конца отнять соответствующие координаты начала. Очевидно, что при смене местами начала и конца вектора, например ВС, у нового, в этом случае СВ, соответвующие координаты будут равны по модулю и противоположны по знаку.
АВ(3-4; 2-9; 5+1), АВ(-1; -7; 6), => BA(1; 7; -6)
AC(-4-4; -5-9; 4+1), AC(-8; -14; 5) => CA(8; 14; -5)
AD(-3-4; 2-9; -2+1), AD(-7; -7; -1) => DA(7; 7; 1)
ВС(-4-3; -5-2; 4-5), ВС(-7; -7; -1) => CB(7; 7; 1)
BD(-3-3; 2-2; -2-5), BD(-6; 0; -7) => DB(6; 0; 7)
CD(-3+4; 2+5; -2-4), CD(1; 7; -6) => DC(-1; -7; 6)
Равные векторы имеют равные координаты, такие пары AB и DC, BA и CD, AD и BC, DA и CB.
B2. Дан ΔABC, точка M — середина стороны AB, точка N — середина стороны BC,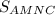 = 60. Найти
= 60. Найти 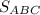 .
.
MN || AB, MN =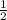 AB ⇒ ∠BMN = ∠BAC ⇒ ΔBMN подобный ΔBAC.
AB ⇒ ∠BMN = ∠BAC ⇒ ΔBMN подобный ΔBAC.
ответ: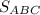 = 80 ед. кв.
= 80 ед. кв.
B3. AK — биссектриса ΔABC, АВ = 4, ВК = 2, КС = 3. Найти периметр ΔABC.
Биссектриса угла делит противоположную сторону на отрезки, пропорциональные прилегающим сторонам:
P = AB+AC+(BK+CK)
P = 4+6+(2+3) = 15
ответ: Периметр ΔАВС равен 15.
B4. Площадь прямоугольного ΔABC равна 360 см², АС:ВС = 3:4. Из середины гипотенузы восстановлен перпендикуляр КМ. Найти площадь ΔMKC.
BK = CK =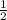 BC
BC
∠ABC = ∠KMC ⇒ ΔCKM и ΔCAB подобны по двум углам и пропорциональной стороне.
ответ: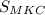 = 160 см².
= 160 см².