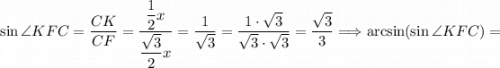Высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому проекций катетов на гипотенузу(или среднему геометрическому тех отрезков на которые высота разбивает гипотенузу).
Можно также использовать ещё одно свойство высоты из прямого угла.
В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
Если высоту обозначить х, то из подобия треугольников составляем пропорцию: х/4 = 9/х, х² = 36, х = 6 см.
Дано: ABCD - тетраэдр, AC = BC = AB = DA = DB = DC, ABK ⊥ CD
Найти: ∠(ABC, ABK) - ?
Решение: Пусть BD = x. Так как по условию AC = BC = AB = DA =
= DB = DC, то x = AC = BC = AB = DA = DB = DC. Проведем из точки K перпендикуляр к прямой AB в точку F. Так как точки A,B ∈ ABC и A,B ∈ ABK, то ABC ∩ ABK = AB.
Так как (F ∈ AB, ABC ∩ ABK= AB ⇒ AB ⊂ ABK) ⇒ F ∈ ABK, то KF ⊂ ABK.
Так как по условию ABK ⊥ CD, то по определению перпендикулярности прямой плоскости, прямая перпендикулярная плоскости, перпендикулярна любой прямой лежащей в этой плоскости, тогда KF ⊥ CD, так как KF ⊂ ABK. Так как KF ⊥ CD и KF ⊥ AB по построению, то по теореме о трех перпендикулярах CF ⊥ AB.
Так как CF ⊥ AB и KF ⊥ AB, то угол ∠KFC является линейным углом двухгранного угла ∠(ABC, ABK), то есть ∠(ABC, ABK) = ∠KFC.
Так как по условию AC = BC = AB = DA = DB = DC, то тетраэдр ABCD - правильный по определению. По свойствам правильного тетраэдра все его грани правильные треугольники, тогда треугольник ΔABC - правильный. По свойствам правильного треугольника все его углы равны 60°, тогда ∠CAB = 60°. Рассмотрим треугольник ΔCAF. Так как CF ⊥ AB, то треугольник ΔCAF - прямоугольный. . Так как CF ⊥ AB, то CF - высота правильного треугольника ΔABC. По свойствам правильного треугольника все его высоты являются медианами и биссектрисами, тогда точка F - середина отрезка AB. Так как все грани правильного тетраэдра правильные треугольники, то треугольник ΔADB - правильный. Проведем отрезок DF в треугольнике ΔΔADB. Так как точка F - середина отрезка AB, то отрезок DF - медиана, а по свойствам правильного треугольника биссектриса и высота. Так как по свойствам правильного тетраэдра(ABCD) все его грани равны между собой треугольник, то соответствующие элементы треугольников равны, тогда CF = DF как высоты правильных треугольников, следовательно треугольник ΔCFD - равнобедренный с основанием CD. Так как FK ⊥ CD, то по теореме высота равнобедренного треугольника проведенная к основанию(CD) является медианой и биссектрисой, то есть
Высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому проекций катетов на гипотенузу(или среднему геометрическому тех отрезков на которые высота разбивает гипотенузу).
Можно также использовать ещё одно свойство высоты из прямого угла.
В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
Если высоту обозначить х, то из подобия треугольников составляем пропорцию: х/4 = 9/х, х² = 36, х = 6 см.
Объяснение:
Дано: ABCD - тетраэдр, AC = BC = AB = DA = DB = DC, ABK ⊥ CD
Найти: ∠(ABC, ABK) - ?
Решение: Пусть BD = x. Так как по условию AC = BC = AB = DA =
= DB = DC, то x = AC = BC = AB = DA = DB = DC. Проведем из точки K перпендикуляр к прямой AB в точку F. Так как точки A,B ∈ ABC и A,B ∈ ABK, то ABC ∩ ABK = AB.
Так как (F ∈ AB, ABC ∩ ABK= AB ⇒ AB ⊂ ABK) ⇒ F ∈ ABK, то KF ⊂ ABK.
Так как по условию ABK ⊥ CD, то по определению перпендикулярности прямой плоскости, прямая перпендикулярная плоскости, перпендикулярна любой прямой лежащей в этой плоскости, тогда KF ⊥ CD, так как KF ⊂ ABK. Так как KF ⊥ CD и KF ⊥ AB по построению, то по теореме о трех перпендикулярах CF ⊥ AB.
Так как CF ⊥ AB и KF ⊥ AB, то угол ∠KFC является линейным углом двухгранного угла ∠(ABC, ABK), то есть ∠(ABC, ABK) = ∠KFC.
Так как по условию AC = BC = AB = DA = DB = DC, то тетраэдр ABCD - правильный по определению. По свойствам правильного тетраэдра все его грани правильные треугольники, тогда треугольник ΔABC - правильный. По свойствам правильного треугольника все его углы равны 60°, тогда ∠CAB = 60°. Рассмотрим треугольник ΔCAF. Так как CF ⊥ AB, то треугольник ΔCAF - прямоугольный.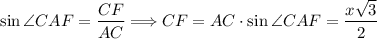
. Так как CF ⊥ AB, то CF - высота правильного треугольника ΔABC. По свойствам правильного треугольника все его высоты являются медианами и биссектрисами, тогда точка F - середина отрезка AB. Так как все грани правильного тетраэдра правильные треугольники, то треугольник ΔADB - правильный. Проведем отрезок DF в треугольнике ΔΔADB. Так как точка F - середина отрезка AB, то отрезок DF - медиана, а по свойствам правильного треугольника биссектриса и высота. Так как по свойствам правильного тетраэдра(ABCD) все его грани равны между собой треугольник, то соответствующие элементы треугольников равны, тогда CF = DF как высоты правильных треугольников, следовательно треугольник ΔCFD - равнобедренный с основанием CD. Так как FK ⊥ CD, то по теореме высота равнобедренного треугольника проведенная к основанию(CD) является медианой и биссектрисой, то есть
CK = KD = CD : 2 = x : 2 = 0,5x.
Рассмотрим прямоугольный треугольник ΔCKF.