Табандарының ауданы бірдей екі цилиндерінің біреуі мыстан биіктігі 6 см ға тең никелден жасалған . Олар горизонталь жазықтыққа бірдей қысым жібереді . Мыс цилиндерінің биіктігі қандай? p m=8900 кг /м³ p n=8900 кг/м³​

KK₁ = 3 ед.

Объяснение:

Дано: прямая АВ;

АК=КВ;

АА₁ ⊥ АВ; ВВ₁ ⊥ АВ; КК₁ ⊥ АВ.

АА₁ = 5; ВВ₁ = 11.

Найти: КК₁

Пусть А₁В₁= 2а.

Если две прямые перпендикулярны третьей, то они параллельны между собой.

АА₁ ⊥ АВ; ВВ₁ ⊥ АВ; КК₁ ⊥ АВ ⇒ АА₁ || ВВ₁ || КК₁.

Теорема Фалеса:

Если на одной из двух прямых отложить последовательно несколько равных между собой отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

АК = КВ ⇒ А₁К₁ = К₁В₁ = а.

Рассмотрим ΔА₁АО и ΔОВВ₁ - прямоугольные.

Вертикальные угла равны.

∠1 = ∠2 (вертикальные)

⇒ ΔА₁АО ~ ΔОВВ₁  (по двум углам)

Составим пропорцию:

Пусть А₁О = 5х, тогда ОВ₁ = 11х

Составим уравнение:

⇒

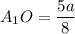
Тогда

Рассмотрим ΔА₁АО и ΔК₁КО - прямоугольные.

∠1=∠2 (вертикальные)

⇒ ΔА₁АО ~ ΔК₁КО

Составим пропорцию:

    Сколько плоскостей можно провести через 2 точки?

ответ: бесчисленное множество.

Объяснение:    Из аксиом планиметрии: Через любые две точки можно провести прямую и притом только одну.

Через две данные точки – ( А и В )– проходит единственная прямая (а ) (см. рисунок).

    Из аксиом стереометрии: Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.

  Через точки (А и В) лежащие на прямой ( а ),  и через каждую точку ( b, c, d…..n ), не лежащую на этой прямой, проходит одна плоскость ( b, c, d…..n ). В пространстве точек, не лежащих на данной прямой.  бесчисленное множество, следовательно, через две точки можно провести прямую и провести бесчисленное множество плоскостей.

  Для наглядности можно представить себе сферу и плоскости сечения, проходящие через её диаметр  и каждую точку на её поверхности.