Задача: Вне плоскости прямоугольника ABCD взяты точки M, причем MA⊥AB и MA⊥AD. Найти градусную меру угла между прямой MC и плоскостью ABC, если AB = 1 см, AD = √2 см, AM = 1 см.
ΔAMC — прямоугольный, ∠MAC = 90°, т.к. MA⊥AB и MA⊥AD ⇒ MA⊥ABCD и MA⊥ABC.
AC — диагональ ABCD и проекция MC на плоскость ABC.
∠ACM — угол между прямой MC и плоскостью ABC.
AD = BC = √2 см; AB = CD = 1 см, т.к. ABCD — прямоугольник.
Найдем AC за т. Пифагора:
Найдем MC за т. Пифагора:
Если катета меньше за гипотенузу в два раза, он лежит напротив угла в 30°. Катет AM = MC ⇒ ∠ACM = 30°.
Объяснение:
1. у него равны 2 стороны(по рисунку) и треугольник; т.к. АОС и ДОС-вертикальные(равен по 2 сторонам и углу)
2.МОN=РОQ(вертикальные)
1=2(по рисунку), и рааная сторона(значит он равен по 2 углам и протеволежащей стороне)
3. одна сторона общая(по римунку), 1=2, 3=4.(равны по 2 углам и протеволежащей стороне)
4. одна сторона общая(по рисунку), 2 равные стороны, и также по рисунку видно, что 1 и 2 равны(по 2 сторонам и углу)
5. две стороны равны, и одна общая(равны по 3 сторонам)
6. 2 стороны равны и 1 общая(по рисунку), значит он равен по 3 сторонам
надеюсь нормально. названия я писать не стала, думаю Вы увидите на рисунке
Задача: Вне плоскости прямоугольника ABCD взяты точки M, причем MA⊥AB и MA⊥AD. Найти градусную меру угла между прямой MC и плоскостью ABC, если AB = 1 см, AD = √2 см, AM = 1 см.
ΔAMC — прямоугольный, ∠MAC = 90°, т.к. MA⊥AB и MA⊥AD ⇒ MA⊥ABCD и MA⊥ABC.
AC — диагональ ABCD и проекция MC на плоскость ABC.
∠ACM — угол между прямой MC и плоскостью ABC.
AD = BC = √2 см; AB = CD = 1 см, т.к. ABCD — прямоугольник.
Найдем AC за т. Пифагора:
Найдем MC за т. Пифагора:
Если катета меньше за гипотенузу в два раза, он лежит напротив угла в 30°. Катет AM =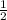
MC ⇒ ∠ACM = 30°.
ответ: Градусную меру угла равна 30°.