сила модуль которой равен 0.5н разложена на две взаимно перпендикулярные составляющие. найдите их модуль если одна из них образует с равнодейтвующей угол 30 градусов
Вот пришло в голову решение :) Так-то задачка ерундовая :) Я продлеваю перпендикуляры HK и HM за точку H до пересечения с BA в точке A1 и BC в точке C1 (ну, точки лежат на продолжениях... из за того, что ∠ABC острый, эти точки есть и лежат где положено :) ) Для треугольника A1BC1 H - точка пересечения высот (ну двух-то точно :) - A1M и C1K), поэтому A1C1 перпендикулярно BH, и, следовательно, параллельно AC; то есть ∠BAC = ∠BA1C; Точки K и M лежат на окружности, построенной на A1C1, как на диаметре, поэтому ∠BA1C + ∠KMC = 180°; как противоположные углы вписанного четырехугольника. Или, что же самое, ∠BA1C = ∠BMK; следовательно ∠BAC = ∠BMK; и треугольники ABC и BMK имеют равные углы. То есть, подобны.
Следствие, которое важнее задачи :) Четырехугольник AKMC - вписанный. То есть через эти 4 точки можно провести окружность.
Дополнение. Тривиальный решения тут такой. ∠KHB = ∠A; ∠MHB = ∠C; BK = BH*sin(A) = BC*sin(C)*sin(A); BM = BH*sin(C) = BA*sin(A)*sin(C); То есть у треугольников ABC и MBK угол B общий, и стороны общего угла пропорциональны BM/BA = BK/BC = sin(A)*sin(B); значит треугольники подобны. коэффициент подобия sin(A)*sin(C), что тоже полезное следствие.
1.) Стороны данного острого угла параллельны плоскости α. Докажите, что и биссектриса параллельна этой плоскости.
2. Прямые a i b которые пересекаются, пересекают три данные параллельные плоскости α, β, γ в точках А₁,А₂,А₃ и В₁,В₂,В₃ соответственно. Найти B₁B₃ ,если А₁А₂=25см, В₂В₃=4 см,А₂А₃+В₁В₂=20 см (на фото рисунок к задачи).
Объяснение:
1)Стороны острого угла определяют плоскость β единственным образом как и пересекающиеся прямые.И эта плоскость β║α ⇒ все прямые плоскости β параллельны α и значит биссектриса угла параллельна α.
2)Пересекающиеся прямы а и в определяют плоскость , которая пересекает плоскости α, β, γ , единственным образом. Линии пересечения плоскостей будут параллельны , т.е. А₁В₁║А₂В₂║А₃В₃ . Введем для простоты записей обозначения А₂А₃=х , В₁В₂=у , тогда х+у=20.
По т. о пропорциональных отрезках , но х=20-у ⇒
, y²-20y+100=0 ,(y-10)²=0 ,y=10
B₁B₃ =B₁B₂+В₂В₃=10+4=14 (cм)
==============================
Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны.
Я продлеваю перпендикуляры HK и HM за точку H до пересечения с BA в точке A1 и BC в точке C1 (ну, точки лежат на продолжениях... из за того, что ∠ABC острый, эти точки есть и лежат где положено :) )
Для треугольника A1BC1 H - точка пересечения высот (ну двух-то точно :) - A1M и C1K), поэтому A1C1 перпендикулярно BH, и, следовательно, параллельно AC;
то есть ∠BAC = ∠BA1C;
Точки K и M лежат на окружности, построенной на A1C1, как на диаметре, поэтому
∠BA1C + ∠KMC = 180°; как противоположные углы вписанного четырехугольника. Или, что же самое, ∠BA1C = ∠BMK;
следовательно ∠BAC = ∠BMK;
и треугольники ABC и BMK имеют равные углы. То есть, подобны.
Следствие, которое важнее задачи :) Четырехугольник AKMC - вписанный. То есть через эти 4 точки можно провести окружность.
Дополнение. Тривиальный решения тут такой.
∠KHB = ∠A; ∠MHB = ∠C;
BK = BH*sin(A) = BC*sin(C)*sin(A);
BM = BH*sin(C) = BA*sin(A)*sin(C);
То есть у треугольников ABC и MBK угол B общий, и стороны общего угла пропорциональны BM/BA = BK/BC = sin(A)*sin(B); значит треугольники подобны.
коэффициент подобия sin(A)*sin(C), что тоже полезное следствие.
1.) Стороны данного острого угла параллельны плоскости α. Докажите, что и биссектриса параллельна этой плоскости.
2. Прямые a i b которые пересекаются, пересекают три данные параллельные плоскости α, β, γ в точках А₁,А₂,А₃ и В₁,В₂,В₃ соответственно. Найти B₁B₃ ,если А₁А₂=25см, В₂В₃=4 см,А₂А₃+В₁В₂=20 см (на фото рисунок к задачи).
Объяснение:
1)Стороны острого угла определяют плоскость β единственным образом как и пересекающиеся прямые.И эта плоскость β║α ⇒ все прямые плоскости β параллельны α и значит биссектриса угла параллельна α.
2)Пересекающиеся прямы а и в определяют плоскость , которая пересекает плоскости α, β, γ , единственным образом. Линии пересечения плоскостей будут параллельны , т.е. А₁В₁║А₂В₂║А₃В₃ . Введем для простоты записей обозначения А₂А₃=х , В₁В₂=у , тогда х+у=20.
По т. о пропорциональных отрезках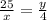
, но х=20-у ⇒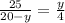 
, y²-20y+100=0 ,(y-10)²=0 ,y=10
B₁B₃ =B₁B₂+В₂В₃=10+4=14 (cм)
==============================
Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны.