В параллелограмме ABCD BD=10 см AB = 12 см. Найдите периметр ΔBOC ( О точка пересечения диагоналей) , если АС - BD = 8 см .
ответ: ( 14+2√17 ) см
Объяснение: АС - BD = 8 (см) ⇒ АС= BD + 8 см =10 см+8 см =18 см
P(ΔBOC) = BO + OC + BC = BD/2 +AC/2 + BC = 5+ 9 +BC = 14 + BC
* * * Диагонали параллелограмма точкой пересечения делятся пополам * * *
Определим сторону BC. Известно: 2(a²+b²) =d₁ ²+d₂²
2(AB² +BC²) =BD² + AC² ⇔ 2(12² +BC²) =10² + 18² ⇒ BC² =68 ;
BC =2√17 см
Окончательно: P(ΔBOC) = ( 14+2√17 ) ( см ) .
Трапеция ABCD с основанием AD вписана в окружность с центром О.Найдите углы трапеции,если ∠AOD=100°,∠BOC=80° и точка О лежит вне трапеции.
Объяснение:
Вписанная в окружность трапеция является равнобедренной.
Значит АВ=CD стягивают равные дуги → ∪AB=∪CD
∠BOC=80° -центральный → ∪ВС=80°
∠AOD=100°--центральный → ∪АВD=100° ⇒ ∪AB=∪CD= =10°.
∠BAD вписанный и опирается на дугу ∪BCD=∪BC+∪CD=80°+10°=90°.
∠BAD=1/2*90°=45°. Значит ∠СDA=45° и ∠СВA=45° (углы при основании равны )
Сумма углов 4-х угольника 360°. Поэтому ∠АВС=∠ВСD= =135°
В параллелограмме ABCD BD=10 см AB = 12 см. Найдите периметр ΔBOC ( О точка пересечения диагоналей) , если АС - BD = 8 см .
ответ: ( 14+2√17 ) см
Объяснение: АС - BD = 8 (см) ⇒ АС= BD + 8 см =10 см+8 см =18 см
P(ΔBOC) = BO + OC + BC = BD/2 +AC/2 + BC = 5+ 9 +BC = 14 + BC
* * * Диагонали параллелограмма точкой пересечения делятся пополам * * *
Определим сторону BC. Известно: 2(a²+b²) =d₁ ²+d₂²
2(AB² +BC²) =BD² + AC² ⇔ 2(12² +BC²) =10² + 18² ⇒ BC² =68 ;
BC =2√17 см
Окончательно: P(ΔBOC) = ( 14+2√17 ) ( см ) .
Трапеция ABCD с основанием AD вписана в окружность с центром О.Найдите углы трапеции,если ∠AOD=100°,∠BOC=80° и точка О лежит вне трапеции.
Объяснение:
Вписанная в окружность трапеция является равнобедренной.
Значит АВ=CD стягивают равные дуги → ∪AB=∪CD
∠BOC=80° -центральный → ∪ВС=80°
∠AOD=100°--центральный → ∪АВD=100° ⇒ ∪AB=∪CD=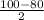 =10°.
=10°.
∠BAD вписанный и опирается на дугу ∪BCD=∪BC+∪CD=80°+10°=90°.
∠BAD=1/2*90°=45°. Значит ∠СDA=45° и ∠СВA=45° (углы при основании равны )
Сумма углов 4-х угольника 360°. Поэтому ∠АВС=∠ВСD=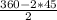 =135°
=135°