2. 1) MY=2 см ( точка Y лежить зліва від точки М на відстані 2 см)
KY=18 см
DY=10 см
2) MY=18 см
KY=2 см ( точка Y лежить зправа від точки К на відстані 2 см)
DY=10 см
Объяснение:
1. Довжина кожного утвореного відрізка дорівнює а
тоді середина такого відрізку дорівнює а
Знаходимо відстань між серединами крайніх відрізків:
L = а+а+а+а+а = а+а = а+а = а = 0,8а
2. Оскыльки МY + KY=16 см, якщо Y лежить на даному выдрізку, а відстань від кінця до середини відрізку 8 смб тоді точка Y лежить на прямій за відрізком
Є 2 випадки, що задовільняють умову задачі:
1) MY=2 см ( точка Y лежить зліва від точки М на відстані 2 см)
KY=18 см
DY=10 см
2) MY=18 см
KY=2 см ( точка Y лежить зправа від точки К на відстані 2 см)
Так как по условию xm+yn=5n, тоxm =(5-y)n если x не равно 0, то разделив левую и правую части уравнения на x, получим m =((5-y)/x) n, где ((5-y)/x) какое-то число.
По условию коллинеарности:Два вектора a и b коллинеарны, если существует число не равное нулю n такое, что a = n · b Следовательно, если a и b не коллинеарны то такого числа не существует. А в нашем примере такое число есть (при x не равном 0). Следовательно если x не равно 0, то векторы коллинеарны. А так как по условию они не коллинеарны, то x = 0. Тогда и y = 0. ответ: x = 0 и y = 0
1. L = 0,8а
2. 1) MY=2 см ( точка Y лежить зліва від точки М на відстані 2 см)
KY=18 см
DY=10 см
2) MY=18 см
KY=2 см ( точка Y лежить зправа від точки К на відстані 2 см)
DY=10 см
Объяснение:
1. Довжина кожного утвореного відрізка дорівнює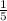
а
тоді середина такого відрізку дорівнює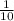
а
Знаходимо відстань між серединами крайніх відрізків:
L =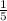
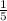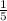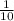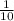а+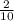
а+
а+
а+
а =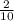 
а+
а =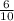 
а+
а =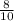 
а = 0,8а
2. Оскыльки МY + KY=16 см, якщо Y лежить на даному выдрізку, а відстань від кінця до середини відрізку 8 смб тоді точка Y лежить на прямій за відрізком
Є 2 випадки, що задовільняють умову задачі:
1) MY=2 см ( точка Y лежить зліва від точки М на відстані 2 см)
KY=18 см
DY=10 см
2) MY=18 см
KY=2 см ( точка Y лежить зправа від точки К на відстані 2 см)
DY=10 см
если x не равно 0, то разделив левую и правую части уравнения на x, получим
m =((5-y)/x) n, где ((5-y)/x) какое-то число.
По условию коллинеарности:Два вектора a и b коллинеарны, если существует число не равное нулю n такое, что a = n · b
Следовательно, если a и b не коллинеарны то такого числа не существует.
А в нашем примере такое число есть (при x не равном 0).
Следовательно если x не равно 0, то векторы коллинеарны.
А так как по условию они не коллинеарны, то x = 0. Тогда и y = 0.
ответ: x = 0 и y = 0