Войти Регистрация Спроси ai-bota

с задачей:

Рівні прямокутники ABCD і ABC1D1 лежать у перпендикулярних площинах. Знайдіть відстань між мимобіжними прямими AD1 і С1D , якщо АВ=15 см, ВС=20 см

Показать ответ

Ответ:

Sheri1

13.07.2021 09:40

1) По теореме Пифагора:

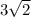$x^2 = 3^2 + 3^2\\\\x = \sqrt{3^2+3^2} = \sqrt{9+9} = \sqrt{18} = \boxed{3\sqrt{2}}$

ответ: $3\sqrt{2}$ .

2) По теореме Пифагора:

$10^2 = x^2 + 6^2\\\\x = \sqrt{10^2-6^2} = \sqrt{100-36} = \sqrt{64} = \boxed{8}$ .

ответ: 8.

3) Диагональ квадрата равна произведению его стороны на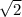 $\sqrt{2}$ , тогда:

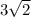$a = \dfrac{d}{\sqrt{2}} = \dfrac{6}{\sqrt{2}} = \sqrt{\dfrac{36}{2}} = \sqrt{18} = \boxed{3\sqrt{2}}$

ответ: $3\sqrt{2}$ .

4) По теореме Пифагора:

$8^2 + x^2 = 10^2\\\\x = \sqrt{10^2 - 8^2} = \sqrt{100 - 64} = \sqrt{36} = \boxed{6}$ .

Площадь прямоугольного треугольника равна полупроизведению его катетов.

$S_{\bigtriangleup} = \dfrac{8\cdot 6}{2} = \dfrac{48}{2} = \boxed{24}$ .

ответ: 6; 24.

5) Треугольник равнобедренный (по условию). В равнобедренном треугольнике высота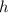 является биссектрисой и медианой. Образовавшиеся два треугольника являются прямоугольными. По теореме Пифагора:

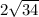$x^2 = h^2 + \left (\dfrac{12}{2}\right )^2 = h^2 + 6^2 = h^2 + 36\\\\x = \sqrt{h^2+36} = \sqrt{10^2 + 36} = \sqrt{100+36} = \sqrt{136} = \boxed{2\sqrt{34}}$

ответ: $2\sqrt{34}$ .

6) Катет, лежащий напротив угла с градусной величиной 30°, равен половине гипотенузы. Пусть - гипотенуза этого треугольника. По теореме Пифагора:

$c^2 = a^2 + x^2 =\\\\x = \sqrt{c^2 - a^2} = \sqrt{c^2 - \left (\dfrac{c}{2}\right )^2} = \sqrt{c^2 - \dfrac{c^2}{4}} = \sqrt{\dfrac{3c^2}{4}} = \boxed{\dfrac{c\sqrt{3}}{2}}$

Больше сделать здесь ничего нельзя, поскольку длина гипотенузы нам не дана. Но если бы она была дана, то длину катета можно было бы вычислить через эту формулу.

0,0(0 оценок)

Ответ:

xujixixud

23.06.2020 18:41

Периметр ромба равен 8 м.

Объяснение:

В ромбе диагонали взаимно перпендикулярны и являются биссектрисами углов. Следовательно ∠KEL = ∠EKL.

∠EOA = ∠EKL (дано). =>

∠KEL = ∠EAO => треугольник EOA равнобедренный.

Кроме того, АВ║LK║EF (так ∠EOA = ∠EKL соответствкнные углы при АВ и LK и секущей ЕК).

Значит ЕА = АО =1м.

АО = ОВ (так как точка О - точка пересечения диагоналей ромба).

AEFB - параллелограмм (так как АВ║EF и EA║FB). =>

EF =AB = 2·AO = 2 м.

Итак, сторона ромба равна 2м, тогда его периметр равен 8м (стороны ромба равны).

0,0(0 оценок)

Популярные вопросы: Геометрия

alonedango

16.05.2021 15:18

Сторона bс параллелограмма abcd вдвое больше стороны cd. точка l середина стороны bc. докажите, что dl-биссектриса угла cds...

лчлвоу

06.02.2021 22:30

Составьте уравнение прямой проходящей через 2 точки (9; 10) (5; -4) много...

пандос3

01.06.2022 11:15

Найдите координаты центра окружности и её радиус, если известно уравнение окружности: x^2+(y-4)^2=8...

Danielllllllll

13.02.2023 01:57

Длина окружности основания цилиндра равна 8 . площадь боковой поверхности равна 20 . найдите высоту цилиндра...

роза413

09.02.2021 14:37

Геометрия 7 класс очень нужно Всем...

costa174rus

29.06.2021 01:01

Точки A и C лежат в плоскости a. Точки B и D лежат в плоскости b. Какие из прямых AC, CD, BD, AB, BC и AD пересекают плоскость b?...

Foret228

08.05.2020 02:42

Из точки d, принадлежащей гипотенузе ab прямоугольного треугольника abc, проведены две прямые, параллельные катетам. сумма периметров получившихся треугольников akd и...

RageTeenage

08.05.2020 02:42

Найди среднюю линию трапеции, если ее площадь равна 8,6 см, а высота 4,3 см....

Ника7002

08.05.2020 02:42

Найдите величину каждого из углов, образовавшихся при пересечении двух прямых, если: сумма трёх из них равна 228°...

PAMAGITE12

08.05.2020 02:42

На плоскости дан отрезок ab и на нём произвольная точка m. на отрезках am и mb как на сторонах построены квадраты acd и mbef, лежащие по одну сторону от ab, и n - точка...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку