с геометрией.
В трапеции ABCD угол А = 60°, угол D = 45°, основание ВС равно 5 см, BF и СЕ - высоты трапеции, ED = 4 см. Найдите площадь трапеции.
С решением не только ответ!

Показать ответ

Ответ:

lilyamkrtchyan1

16.02.2021 16:59

S треугольника всегда = высота*основание к которому она проведена разделить это всё на два. (h*осн.)/2

1) высота - 6, основание 12, значит площадь - 12*6/2= 72/2=36 - Б

2)Если в треугольнике есть угол в 30 градусов, то сторона напротив него - в два раза меньше гипотенузы ( стороны напротив прямого=90 угла).

Тут гипотенуза = 12 значит сторона напротив угла равна 12/2 = 6. Чтобы найти вторую сторону используем теорему Пифагора.

a^2+b^2=c^2

где а и б - стороны, а с - гипотенуза. Подставим известное...

6^2+b^2=12^2

36+B^2=144

b^2=144-36

b^2=108

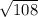
b = $\sqrt{108}$

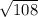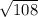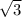Площадь треугольника здесь - 6* $\sqrt{108}$ /2 = 3* $\sqrt{108}$ =18 $\sqrt{3}$ -в

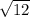3)Опустим высоту. Найдём её тоже через свойство угла в 30 градусов и теорему пифагора. 16-4=12 значит высота $\sqrt{12\\}$ . в итоге.

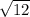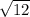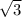площадь= $\sqrt{12}$ *6=6 $\sqrt{12}$ =12 $\sqrt{3}$ - в

4)Наименьшая высота будет опущена к самой большой стороне, запомни. Опустим ее к стороне 20. Через формулы ( набери в инете среднее геометрическое, долго оформлять очень ) найдём, что x=12,8 - кусочек, которой получается в результате деления высотой стороны двадцать, который ближе к стороне 16. Аналогично найдём и кусочек, ближний к стороне 12. y=7,2. Высота равна корню произведения xy= 9,6 - высота - г

0,0(0 оценок)

Ответ:

matfeys

21.05.2021 08:18

1) Чтобы найти координаты вектора AС, зная координаты его начальной точки А и конечной точки С, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки. То есть:

AС = (Сx - Ax; Сy - Ay) = (5 - 1; -2 - (-2)) = (4; 0).

Таким же найдем координаты вектора ВА:

BA = (Ax - Bx; Ay - By) = (1 - 3; -2 - 6) = (-2; -8).

2) Точка М расположена на отрезке ВС и делит его пополам, следовательно, для поиска координат точки М необходимо определить координаты отрезка ВС и разделить их пополам, то есть:

М = ВС / 2 = (Сx + Bx; Сy + By) / 2 = ((Сx + Bx) / 2; (Сy + By) / 2) = ((5 + 3) / 2; (-2 + 6) / 2) = (8 / 2; 4 / 2) = (4; 2).

Для вычисления длины отрезка воспользуемся формулой вычисления расстояния между двумя точками A (xa; ya) и B (xb; yb):

AB = √(( xb - xa)^2 + (yb - ya)^2).

Подставим значения точки А (1; -2) и М (4; 2) в формулу:

AM = √((4 - 1)^2 + (2 - (-2))^2) = √(3^2 + 4^2) = √(9 + 16) = √25 = 5.

ответ: координаты вектора АС (4; 0), вектора ВА (-2; -8), координаты точки М (4; 2), длина отрезка АМ = 5.

Объяснение:

0,0(0 оценок)

Популярные вопросы: Геометрия