Розв'язати:
Варіант 1
Тестове завдання 8
19. Які з ламаних, що мають наведені довжини ланок, можуть бути замкненими?
А. 1 дм, 2 дм, 3 дм, 7 дм.
B. 8 м, 9 м, 10 м, 24 м.
Б. 3 см, 4 см, 5 см, 7 см, 19 см.
Г. 15 мм, 18 мм, 20 мм, 25 мм, 80 мм.
29. Скільки сторін має многокутник, у якого число діагоналей, проведених з однієї вершини, дорівнює 7?
A. 9.
Б. 10.
B. 8.
Г.7.
39. Чому дорівнює сума внутрішніх кутів опуклого восьмикутника?
A. 1440°.
Б. 1080°.
Г. 1260°.
B. 900°.
4. Радіус кола, описаного навколо прямокутника, дорівнює 20 мм. Чому дорівнює відстань між серединами двох суміжних сторін прямокутника?
А. 10 мм.
Б. 20 мм.
Г.5 мм.
В. 40 мм.
5. Сторони паралелограма дорівнюють 4,2 см і 5,6 см. Висота, проведена до більшої зі сторін, дорівнює 3,3 см. Чому дорівнює друга висота цього паралелограма?
А. 18,48 см.
В. 7 55 см.
Б. 13,86 см.
Г. 4,4 см.
6. Яку фігуру утворюють вершини рівновеликих трикутників, що мають спільну основу AB ?
А. Коло, діаметр якого дорівнює основі AB; Б. Дві прямі, паралельні основі AB; В. Два промені, паралельні основі AB; Г. Два відрізки, паралельні основі AB.
7*. Якою є площа гострокутного трикутника, якщо його висота, проведена до основи, дорівнює 6 см, а проекції бічних сторін на цю основу дорівнюють 12 см i4 см?
А. 48 см.
г. 144 см.
В. 12см.
Б. 36 см.
8*. У квадрат, площа якого дорівнює 64 см“, вписано коло. Яким є радіус цього кола?
А. 32 см.
Б. 16 см.
Г. 4 см.
B. 8 см.
9++. Обчисліть площу зображеної фігури й позначте правильну відповідь.
А. 120 см.
Г. нша відповідь.
В. 100 см.
Б. 960 см.
10*я. Три кути опуклого многокутника дорівнюють по 80°, усі інші — по 150°.
Скільки вершин має цей многокутник?
A. 5.
Б. 6.
B. 7.
Г. 8.
11**. Який з усіх паралелограмів з діагоналями, що дорівнюють 4см і 8 см, має найбільшу площу?
А. Прямокутник. Б. Квадрат.
Г. Паралелограм.
В. Ромб.
12**. Периметр описаної навколо кола трапеції дорівнює 30 см. Яка довжина середньої лінії цієї трапеції?
А. 15 см.
Б. 10 см.
Г. Не можна визначити.
В. 7,5 см.
А по свойству касательных к окружности ВН= ВТ, СН = СМ, значит АТ = АМ = 25 - 7 = 18, значит рассмотрим подобие треугольников АВС и АМТ, у них: общий угол А, МТ // (параллельно) ВС, значит коэффициент подобия = 25/18 (большой - АВС : маленький - АМТ), значит сторона ВС относится к стороне МТ как 25/18, значит 14/х=25/18
Так как не уточнено, как именно располагается угол 30 градусов относительно катета в 24 см, то возможно два варианта решения. Они различаются только цифрами, а суть одна.
Прямоугольный треугольник в основании. Один катет равен 24. Прилежащий угол равен 30 градусов. Найдем гипотенузу:
cos30 = 24/гипотенузу.
гипотенуза =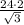 =
= 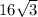 .
.
второй катет по теореме Пифагора будет равен:
катет2 =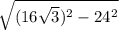 =
= 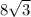 .
.
площадь прямоугольного треугольника в основании:
S(тр) =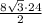 =
= 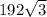
ТАких треугольников в призме 2.
Сама призма - прямая, значит грани перпендикулярны оснвоанию. Большая боковая грань будет опираться на гипотенузу. Ее диагональ находится к плоскости основания под углом 45 градусов. Треугольник образованный высотой призмы, этой диагональю и гипотенузой будет прямоугольным и равнобедренным. (один угол 90, на два дргуих остается 90, Раз один из них равен 45, то и второй тоже будет 45). Из всего этого следует, что высота призмы численно арвна гипотенузе -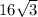 .
.
Находим площадь грани, опирающей на гипотенузу:
этот прямоугольник =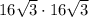 = 768.
= 768.
площадь грани, опирающейся на катет 24 см:
S =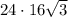 =
= 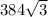
площадь грани, опирающейся на катет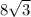 :
:
S =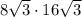 = 384.
= 384.
Теперь суммируем все площади и получаем полную боковую поверхность призмы:
S(полн) =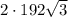 + 768 +
+ 768 + 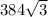 + 384 =
+ 384 = 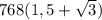
Угол 30 градусов в треугольнике основания является противолежащим относительно катета 24 см.
Тогда гипотенуза вдвое больше катета:
гипотенуза = 24*2 = 48.
второй катет = =
= 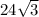 .
.
Так как треугольник в основании приумиды равен верхнему, то можно сразу найти их суммарную площадь (площадь одного треугольника = произведению катетов, деленному на2, а их сумма - это все равно, что помножить площадь одного треугольника на 2, то есть 2 сокращается).
S(обоих тр) =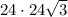 =
= 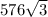
Высота призмы = 48.
Площадь прямоугольника, опирающегося на гипотенузу:
S = (48*48) = 2304.
площадь прямоугольника, опирающегося на катет 24 см:
S = 24*48 = 1152
площадь прямоугольника, опирающегося на второй катет:
S =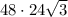 =
= 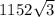
S(общая) =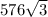 + 2304 + 1152 +
+ 2304 + 1152 + 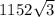 =
= 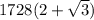
Полные выкладки делать некогда, поэтому советую числа перепроверить, потому как решала быстро.