Найдите площадь треугольника, две стороны которого равны 6 и 8, а медиана, заключённая между ними, равна 5.
▔ ▔ ▔
★☆★ Чертёж смотрите во вложении ★☆★
ΔАВС.
АВ = 6.
ВС = 8.
ВО — медиана = 5.
S(ΔАВС) = ?
Достроим ΔАВС до параллелограмма ABCD как показано на рисунке.
▸Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам◂
Следовательно —
Тогда —
▸Противоположные стороны параллелограмма равны◂
AD и ВС — противоположные стороны.
Рассмотрим ΔABD.
▸Если сумма квадратов двух сторон равна квадрату большей стороны, то такой треугольник — прямоугольный (теорема, обратная теореме Пифагора)◂
Проверим стороны ΔABD —
Подставим известные нам численные значения —
Мы получили верное равенство, следовательно, ΔABD — прямоугольный (∡A = 90°).
▸Если в параллелограмме один угол прямой, то этот параллелограмм — прямоугольник◂
То есть, параллелограмм ABCD — прямоугольник.
Тогда, по определению прямоугольника —
∡А = ∡В = ∡С = ∡D = 90°.
Рассмотрим ΔАВС — прямоугольный.
▸Площадь прямоугольного треугольника равна половине произведения его катетов◂
Подставим в формулу известные нам численные значения —
24 (ед²).
Найти: ∠ABC, ∠BCA, ∠BAC - ?
Пусть ∠BAC = 2x.
Тогда ∠BCA = ∠BAC = 2x.
Поэтому ∠BAF = ∠CAF = ∠BAC:2 = x.
ΔAFC - равнобедренный т.к. AF=AC.
∠AFC = ∠ACF = 2x, как углы при основании.
В ΔAFC:
∠AFC+∠ACF+∠CAF = 180°;
2x+2x+x = 180°;
5x = 180°;
2x = 180°:5·2 = 72°.
∠BCA = ∠BAC = 2x = 72°;
В ΔABC:
∠ABC+∠BCA+∠BAC = 180°;
∠ABC = 180°-72°-72°;
∠ABC = 36°.
ответ: 36°, 72° и 72°.
Найдите площадь треугольника, две стороны которого равны 6 и 8, а медиана, заключённая между ними, равна 5.
▔ ▔ ▔
★☆★ Чертёж смотрите во вложении ★☆★
Дано:ΔАВС.
АВ = 6.
ВС = 8.
ВО — медиана = 5.
Найти:S(ΔАВС) = ?
Решение:Достроим ΔАВС до параллелограмма ABCD как показано на рисунке.
▸Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам◂
Следовательно —
Тогда —
▸Противоположные стороны параллелограмма равны◂
AD и ВС — противоположные стороны.
Следовательно —
Рассмотрим ΔABD.
▸Если сумма квадратов двух сторон равна квадрату большей стороны, то такой треугольник — прямоугольный (теорема, обратная теореме Пифагора)◂
Проверим стороны ΔABD —
Подставим известные нам численные значения —
Мы получили верное равенство, следовательно, ΔABD — прямоугольный (∡A = 90°).
▸Если в параллелограмме один угол прямой, то этот параллелограмм — прямоугольник◂
То есть, параллелограмм ABCD — прямоугольник.
Тогда, по определению прямоугольника —
∡А = ∡В = ∡С = ∡D = 90°.
Рассмотрим ΔАВС — прямоугольный.
▸Площадь прямоугольного треугольника равна половине произведения его катетов◂
Следовательно —
Подставим в формулу известные нам численные значения —
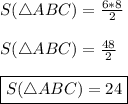
ответ:24 (ед²).
Найти: ∠ABC, ∠BCA, ∠BAC - ?
Пусть ∠BAC = 2x.
В равнобедренном треугольника углы при основании равны.Тогда ∠BCA = ∠BAC = 2x.
Биссектриса делит угол на два равных.Поэтому ∠BAF = ∠CAF = ∠BAC:2 = x.
ΔAFC - равнобедренный т.к. AF=AC.
∠AFC = ∠ACF = 2x, как углы при основании.
Сумма углов треугольника равна 180°.В ΔAFC:
∠AFC+∠ACF+∠CAF = 180°;
2x+2x+x = 180°;
5x = 180°;
2x = 180°:5·2 = 72°.
∠BCA = ∠BAC = 2x = 72°;
В ΔABC:
∠ABC+∠BCA+∠BAC = 180°;
∠ABC = 180°-72°-72°;
∠ABC = 36°.
ответ: 36°, 72° и 72°.