Обозначим центр малой окружности через . Если окружность касается хорды, то по свойствам касательной радиус окружности перпендикулярен хорде в этой точке: .
Если отрезок перпендикулярен хорде, то при их пересечении он делит хорду пополам (это теорема, которую изучают в школе). Значит, точка — середина хорды . Треугольник равнобедренный (поскольку отрезки и равны как радиусы). Значит, медиана является также и высотой. Получим, что . Учитывая предыдущее равенство, получим, что . Это значит, что точки и лежат на одной прямой. Тогда на той же прямой лежит точка касания (ведь по условию она диаметрально противополож
Пусть в тр-ках авс и а (1)в (1)с (1) 1) равны медианы вк и в (1)к (1) , 2) угол авк =углу а (1)в (1)к (1) 3) угол свк = углу с (1)в (1)к (1) доказать, что тр-к авс = тр-ку а (1)в (1)с (1) доказательство в тр-ке авс продолжим медиану вк и отложим км =вк и точку м соединим с точками а и с аналогичные построения сделаем в тр-ке а (1)в (1)с (1), тогда вм =в (1)м (1) 1) тр-к акв =тр-ку скм ( по двум сторонам вк=км и ак=кс и углу между ними -они вертикальные) 2) аналогично тр-к а (1)к (1)в (1) =тр-ку с (1)к (1)м (1) отсюда следует 3) ав=мс =а (1)в (1) =м (1)с (1), < авм = < вмс =< а (1)в (1)м (1) = < в (1)м (1)с (1) 4) тогда тр-к всм = тр-ку в (1)с (1)м (1) по стороне вм =в (1)м (1) и двум прилежащим углам 5) отсюда вс =в (1)с (1) и ав=мс =а (1)в (1) =м (1)с (1), 6) проэтому тр-к авс = тр-ку а (1)в (1)с (1) по двум сторонам и углу между ними второй способ состоит в том, что по теореме " площадь тр-ка равна половине произведения двух сторон на синус угла между ними выражают стороны ав и вс через медиану вк и углы авк и свк применяя соотношение s (авс) = s (авк) + s (свк) и доказывают, что ав= а (1)в (1) и вс= в (1)с (1)
См. рисунок.
Обозначим центр малой окружности через . Если окружность касается хорды, то по свойствам касательной радиус окружности перпендикулярен хорде в этой точке:
. Если окружность касается хорды, то по свойствам касательной радиус окружности перпендикулярен хорде в этой точке: 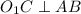 .
.
Если отрезок перпендикулярен хорде, то при их пересечении он делит хорду пополам (это теорема, которую изучают в школе). Значит, точка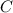 — середина хорды
— середина хорды 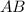 . Треугольник
. Треугольник 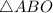 равнобедренный (поскольку отрезки
равнобедренный (поскольку отрезки 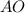 и
и 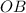 равны как радиусы). Значит, медиана
равны как радиусы). Значит, медиана 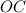 является также и высотой. Получим, что
является также и высотой. Получим, что 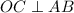 . Учитывая предыдущее равенство, получим, что
. Учитывая предыдущее равенство, получим, что 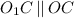 . Это значит, что точки
. Это значит, что точки 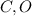 и
и  лежат на одной прямой. Тогда на той же прямой лежит точка касания
лежат на одной прямой. Тогда на той же прямой лежит точка касания 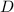 (ведь по условию она диаметрально противополож
(ведь по условию она диаметрально противополож