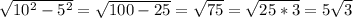Решить(полнлстью решение, как вы пршли к такому выводу): 1. треугольник мав и квадрат авсd имеют общую сторону ав и их плоскости взаимно перпендикулярны.найти угол mаd? 2.в прямоугольном параллелепипеде основанием служит квадрат. диагональ параллелепипеда равна 10 см. и составляет с плоскостью боковой угол 60 градусов. найти стороны основания? вот такого не надо: 1.угол будет равен 90 градусов. 2.стороны основания равнв 5корень из 2 деленое все на
2)Зная,что угол между диогональю паралепипеда и диогональю квадрата рвен 60 градусам имеем,cos(60)=x/10
где х диогонал квадрата =>
cos(60)=0.5
X=5,теперб мнимо делим квадрат на два треугольника,где диогональ квадрата является гипотенузой квадратов.=>
a^2+a^2=5^2=>
2a^2=25
a= корень из 12.5ну стороны квадрата всегда были одинак.
1)Плоскости МАВ и АВСD пересекаются по прямой АВ. Поскольку МАВ и АВСD перпендикулярны, то МА перпендикулярно АВ и АD перпендикулярно АВ, то МА перпендикулярно АD(как три взаемноперпендикулярных прямых)
Значит MАD=90 градусов.
2) Пускай нижняя основа ABCD, а верхняя A1B1C1D1.
С треугольника A1D1D найдём DD1:
DD1=A1D/2(за свойствами катета, который лежит напротив угла 30 градусов)
DD1=5
С треугольника AD1D найдём АD:
АD=