решить
1 . Прямая АМ касается окружности с центром в точке О.
А – точка касания. Найдите ОМ, если АО = 15см, АМ = 20см.
2. В треугольнике АВС АВ=12см, ВС=9см, АС=15 см. Докажите, что АВ- отрезок
касательной, проведенной из точки А к окружности с центром в точке С и радиусом,
равным 9 см.
Дано:
Усеченный конус
Sосн₁ = 9π см²
Sосн₂ = 100π см²
Sсеч = 312π см²
--------------------------------
Найти:
h - ?
1) Сначала мы найдем радиусы окружности верхнего и нижнего усеченного конуса используя площадь круга:
Sосн₁ = πr² ⇒ r = √Sосн₁/π = √9π см²/π = √9 см² = 3 см ⇒ BO₁ = BC = 3 cм
Sосн₂ = πR² ⇒ R = √Sосн₁/π = √100π см²/π = √100 см² = 10 см ⇒ AO = OD = 10 см
2) Равнобедренная трапеция ABCD является осевым сечением данного усеченного конуса: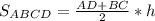
3) В трапеции ABCD:
AD = 2AO = 2R = 2×10 см = 20 см
BC = 2BO₁ = 2r = 2×3 см = 6 см
4) И теперь находим высоту равнобедренной трапеций ABCD:
ответ: h = 24 см
P.S. Рисунок показан внизу↓
Объяснение:
10) Здесь можем провести прямую через точки N и P, лежащие в одной плоскости (A1B1C1). Ее след — NP (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.
Продолжим прямую NP. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и P. Еще две прямые этой плоскости — C1D1 и A1D1 . Точка пересечения A1D1 и NP — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( DCC1), а значит, через нее и точку M, лежащую в этой же плоскости, можно провести прямую. Прямая MS пересекает ребро DD1 в точке E. ME — ее след (видимый). Через точки P и E, лежащие в одной плоскости (DCC1), можно провести прямую, след которой — PE (видимый). В плоскости (DCC1) есть прямая PE, в параллельной ей плоскости (ABB1) — точка M. Через точку M можем провести прямую ML, параллельную PE. Она пересекает ребро BB1 в точке L. ML — след этой прямой (невидимый). Точки N и L лежат в одной плоскости (BCC1), значит, через них можно провести прямую. Ее след — NL (невидимый). Пятиугольник MLNPE — искомое сечение.
3) Здесь точки M и N лежат в одной плоскости ABS, соединяем их, получившийся след MN (видимый). Точки M и P лежат в одной плоскости APS, соединяем их, получаем прямую, след которой MP (невидимый). Точки N и P лежат в одной плоскости ABP, соединяем их, получаем прямую, след которой NP (невидимый). Треугольник NPM - искомое сечение.
Всё просто))) Надеюсь понятно объяснил