Расстояния от вершин А, В, С параллелограмма ABCD, не пересекающего плоскость а до плоскости а равны соответственно 4 см, 6 см и 23 см. Найдите расстояние от вершины D до плоскости а .
DC и АВ-основания трапеции ABCD, точка Е-середина стороны ВС. На средней линии трапеции выбрана точка F так, что CDFE-параллелограмм . Известно , что S(ABCD)=38 см² и S(CDFE)=10 см² . Найдите площадь четырехугольника DAEF.
Объяснение:
S(DAEF)=S(DAE)-S(DFE), чертеж 1 . Продолжим часть средней линии трапеции → МЕ.
1) Чертеж 2 ; S(DAE)=S(DЕМ) +S(АЕМ)=
= (опустим высоты Δ DEM, ΔAEM)=
=1/2*МЕ*DP+1/2*ME*AH=1/2*ME*(DP+AH)=( сумма высот
треугольников будет равна высоте трапеции)=1/2*ME*h=
=1/2 * *h=1/2*S(ABCD)=1/2*38=19(cм²).
2)S(DFE)=( диагональ параллелограмма делит его на два
Построение выполняется с циркуля и линейки . 1. Строим прямой угол. Рисуем прямую а (см.рисунок), на ней отмечаем точку О. Справа и слева от точки О на прямой а циркулем откладываем произвольные равные отрезки АО=ОВ. Из точки А радиусом АВ циркулем ппроводим вверх дугу.Из точки В радиусом АВ циркулем проводим вверх дугу. Точку пересечения двух последних дуг -точку С соедим с точкой О. Получили прямую b. Прямые a и b -перпендикулярны. 2.Строим катеты. Из точки О на прямой a вправо циркулем отложим отрезок ОD , равный первому катету. Из точки О на прямой b вверх циркулем отложим отрезок ОЕ, равнй второму катету. Соединим точки Е и D.Треугольник ОЕD построен
DC и АВ-основания трапеции ABCD, точка Е-середина стороны ВС. На средней линии трапеции выбрана точка F так, что CDFE-параллелограмм . Известно , что S(ABCD)=38 см² и S(CDFE)=10 см² . Найдите площадь четырехугольника DAEF.
Объяснение:
S(DAEF)=S(DAE)-S(DFE), чертеж 1 . Продолжим часть средней линии трапеции → МЕ.
1) Чертеж 2 ; S(DAE)=S(DЕМ) +S(АЕМ)=
= (опустим высоты Δ DEM, ΔAEM)=
=1/2*МЕ*DP+1/2*ME*AH=1/2*ME*(DP+AH)=( сумма высот
треугольников будет равна высоте трапеции)=1/2*ME*h=
=1/2 *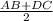
*h=1/2*S(ABCD)=1/2*38=19(cм²).
2)S(DFE)=( диагональ параллелограмма делит его на два
равновеликих треугольника) = 1/2*S(СDFE)=1/2*10=5 (см²).
S(DAEF)=S(DAE)-S(DFE)=19-5=14 (см²) .
1. Строим прямой угол.
Рисуем прямую а (см.рисунок), на ней отмечаем точку О. Справа и слева от точки О на прямой а циркулем откладываем произвольные равные отрезки АО=ОВ. Из точки А радиусом АВ циркулем ппроводим вверх дугу.Из точки В радиусом АВ циркулем проводим вверх дугу. Точку пересечения двух последних дуг -точку С соедим с точкой О. Получили прямую b. Прямые a и b -перпендикулярны.
2.Строим катеты.
Из точки О на прямой a вправо циркулем отложим отрезок ОD , равный первому катету. Из точки О на прямой b вверх циркулем отложим отрезок ОЕ, равнй второму катету. Соединим точки Е и D.Треугольник ОЕD построен