Проведём из вершины В высоту ВН. Она проходя через треугольник АВС будет являться искомым диаметром. Так как ∆АВС равнобедренный, то углы при основании будут равны, поэтому <А=<С=60°. Сумма углов треугольника составляет 180°, поэтому
<В=180–60–60=60°. Все углы этого треугольника равны, поэтому он является равносторонним и АВ=ВС=АС=5√3см.
Радиус описанной окружности вокруг равностороннего треугольника вычисляется по формуле:
Самое простое доказательство:
Нормально геометрическое доказательство:
См. Рисунок.
Согласно определению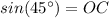 , a
, a 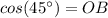
В ΔOAB ∠OAB = 180° - 90° = 45°, значит ΔOAB - равнобедренный с основанием OA.
В ΔOAC ∠OAC = 180° - 90° = 45°, значит ΔOAC - равнобедренный с основанием OA.
ΔOAB = ΔOAC по стороне и двум углам. (OA - общая).
Следовательно OC = OB
Значит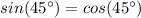
============
Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Успехов в учебе
ответ: диаметр ВН=10см
Объяснение:
Проведём из вершины В высоту ВН. Она проходя через треугольник АВС будет являться искомым диаметром. Так как ∆АВС равнобедренный, то углы при основании будут равны, поэтому <А=<С=60°. Сумма углов треугольника составляет 180°, поэтому
<В=180–60–60=60°. Все углы этого треугольника равны, поэтому он является равносторонним и АВ=ВС=АС=5√3см.
Радиус описанной окружности вокруг равностороннего треугольника вычисляется по формуле:
R=a/√3, где а - сторона треугольника:
R=5√3÷√3=5см;. R=BO=OH
Тогда диаметр ВН=2×5=10см