Радиус окружности, описанной около правильного многоугольника , равен 8см , а радиус вписаной в него окружности 8 см .Найдите :1)сторону многоугольника 2)количество стороно
1) Если один из углов прямоугольного треугольника равен 60°, тогда его второй острый угол будет равен 30°.
2) Катет, лежащий против угла 30°, равен половине гипотенузы, т.к. синус угла 30° = 0.5, а в прямоугольном треугольнике синус угла - это отношение противолежащего ему катета к гипотенузе.
3) Катет, лежащий против угла 60°, равен , где - гипотенуза.
4) Площадь прямоугольного треугольника равна полупроизведению его катетов. Отсюда: . Получаем уравнение:
Так как катет, прилежащий к углу 60°, равен половине гипотенузы (), то он равен 13.
Цитата: СУММА векторов. Начало второго вектора совмещается с концом первого, начало третьего — с концом второго и так далее, сумма же n векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом n-го (то есть изображается направленным отрезком, замыкающим ломаную). РАЗНОСТЬ векторов. Для получения вектора разности (c) = (a-b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b) (вычитаемое), а концом — конец вектора (a) (уменьшаемое). Вектора АВ=-ВА. Решение в приложении.
ответ: 13
Пошаговое решение:
1) Если один из углов прямоугольного треугольника равен 60°, тогда его второй острый угол будет равен 30°.
2) Катет, лежащий против угла 30°, равен половине гипотенузы, т.к. синус угла 30° = 0.5, а в прямоугольном треугольнике синус угла - это отношение противолежащего ему катета к гипотенузе.
3) Катет, лежащий против угла 60°, равен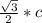 , где
, где  - гипотенуза.
- гипотенуза.
4) Площадь прямоугольного треугольника равна полупроизведению его катетов. Отсюда: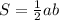 . Получаем уравнение:
. Получаем уравнение:
Так как катет, прилежащий к углу 60°, равен половине гипотенузы ( ), то он равен 13.
), то он равен 13.
РАЗНОСТЬ векторов. Для получения вектора разности (c) = (a-b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b) (вычитаемое), а концом — конец вектора (a) (уменьшаемое).
Вектора АВ=-ВА.
Решение в приложении.