прямые AB и CD пересекаются в одной точке О градусная мера одного из углов обозначенных при пересечении прямых AB и CD равна 50 градусов Найдите градусную меру каждого угла​

Сумма двух углов по одной стороне параллелограмма = 180°
1) если один угол = х°, то другой = 2х (по условию)
    х + 2х = 180
    3х = 180
      х = 60
    2х = 120
Противолежащие углы параллелограмма  равны, 
⇒ углы параллелограмма = 60°; 120°; 60°; 120°

2) Если углы по одной стороне параллелограмма относятся как 4 : 5, значит один угол = 4 частям, то другой угол равен 5 частям.
⇒ 4 + 5 = 9 (частей) составляют 180°
    180 : 9 = 20° приходятся на одну часть
    20 * 4 = 80° - это один угол
    20 * 5 = 100° - это другой угол, 
а т.к. противолежащие углы равны, то углы параллелограмма =
80°; 100°; 80°; 100°.
   

Рассмотрим прямоугольный треугольник SOA в нём радиус описанной окружности основания равен: OA=AB=18. По теореме Пифагора найдем

высоту пирамиды SO.

Теперь рассмотрим прямоугольный треугольник SOK. SK - апофема пирамиды, OK - радиус вписанной окружности основания.

OK = AB√3/2 = 9√3

Тогда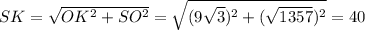

Площадь одной грани (треугольник SBA): S = AB*SK/2 = 18*40/2 = 360

Площадь боковой поверхности пирамиды- это сумма всех площадей грани . В шестиугольной пирамиде граней 6, значит площадь боковой поверхности пирамиды равна: Sбок = 6*360 = 2160

ответ: 2160.