1. Рассмотрим ромб ABCD, лежащий в основании. По свойствам ромба, его диагонали пересекаются под прямым углом и точкой пересечения делятся попопам. Обозначим точку пересечения как O.
2. Рассмотрим треугольник AOD. Он прямоугольный, его катеты AO и OD.
AO = AC/2 = 6/2 = 3 см
OD = BD/2 = 8/2 = 4 см
Найдем гипотенузу AD:
AD =
AD = 5 см
3. Стороны ромба равны, значит, треугольник AOD = AOB = BOC = COD, AB = BC = CD = AD = 5 см.
4. Теперь мы знаем все грани и можем найти площади.
Площадь оснований (площади ромбов) ABCD и A1B1C1D1 рассчитываются по формуле:
S = (AD * BC)/2 = 24 кв.см
Площади граней (всех в силу равенства сторон) - как площади прягоугольников.
Предположим, что существует треугольник (не прямоугольный), в котором две стороны 3 и 4, а площадь равна 6. Тогда на сторону а=4 опускаем высоту из противолежащего угла и записываем: S=1/2*a*h. a=4 => 1/2*4*h=6 => h=3 Но в прямоугольном треугольнике катет (в данном случае высота h=3) не может равняться гипотенузе (в данном случае сторона b=3). Значит изначально треугольник был прямоугольный со сторонами 3 и 4 и гипотенузой, равной 5
2.
Треугольник со сторонами 2,3,4 не является прямоугольным (2^2+3^2=13; значит в прямоугольном треугольнике гипотенуза должна была быть <4).
По теореме косинусов: a^2 = b^2 + c^2 — 2bc · cos α
Осталось подставить числа (известные стороны) и найти единственное неизвестное: cos α
Дано:
параллелепипед ABCDA1B1C1D1
AC = A1C1 = 6 см
BD = B1D1 = 8 см
AA1 = DD1 = CC1 = DD1 = 7 см
1. Рассмотрим ромб ABCD, лежащий в основании. По свойствам ромба, его диагонали пересекаются под прямым углом и точкой пересечения делятся попопам. Обозначим точку пересечения как O.
2. Рассмотрим треугольник AOD. Он прямоугольный, его катеты AO и OD.
AO = AC/2 = 6/2 = 3 см
OD = BD/2 = 8/2 = 4 см
Найдем гипотенузу AD:
AD =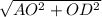
AD = 5 см
3. Стороны ромба равны, значит, треугольник AOD = AOB = BOC = COD, AB = BC = CD = AD = 5 см.
4. Теперь мы знаем все грани и можем найти площади.
Площадь оснований (площади ромбов) ABCD и A1B1C1D1 рассчитываются по формуле:
S = (AD * BC)/2 = 24 кв.см
Площади граней (всех в силу равенства сторон) - как площади прягоугольников.
S = AA1 * AB = 7 * 5 = 35 кв.см
5. Площадь полной поверхности:
S = 2 * 24 + 4 * 35 = 48 + 140 = 188 кв.см
ответ: S = 188 кв.см
Вот и все :) Удачи!
1.
Предположим, что существует треугольник (не прямоугольный), в котором две стороны 3 и 4, а площадь равна 6.
Тогда на сторону а=4 опускаем высоту из противолежащего угла и записываем:
S=1/2*a*h.
a=4 => 1/2*4*h=6 => h=3
Но в прямоугольном треугольнике катет (в данном случае высота h=3) не может равняться гипотенузе (в данном случае сторона b=3).
Значит изначально треугольник был прямоугольный со сторонами 3 и 4 и гипотенузой, равной 5
2.
Треугольник со сторонами 2,3,4 не является прямоугольным (2^2+3^2=13; значит в прямоугольном треугольнике гипотенуза должна была быть <4).
По теореме косинусов: a^2 = b^2 + c^2 — 2bc · cos α
Осталось подставить числа (известные стороны) и найти единственное неизвестное: cos α