Ты же понимаешь, что без чертежа объяснять несколько проблематично? Ну так вот... Наслаждайся! 1) Представь треугольник АВС с прямым углом С. Пусть угол между высотой и ближайшем к ней катетом будет x. Тогда угол между биссектрисой и этим катетом будет 15 + x. Тогда 15 +x +15 +x = 90 ==> х = 30. Рассматривая прямоугольный треугольник, образованный высотой и гипотенузой, можно заметить, что второй его угол будет равен 90 - x = 60. Это один из углов начального треугольника, значит второй угол будет равен 30 (согласен на словах все слишком каряво, так что стоит все это нарисовать) ответ: 30; 60 2) угол 120 градусов может быть только углом, против которого лежит основание. Следовательно, углы при основании равны по 30 градусов. В полученном прямоугольном треугольнике основание - гипотенуза, а высота - катет, лежащий против угла в 30 градусов ==> высота = 4/2 = 2 ответ: 2
1) Представь треугольник АВС с прямым углом С. Пусть угол между высотой и ближайшем к ней катетом будет x. Тогда угол между биссектрисой и этим катетом будет 15 + x. Тогда 15 +x +15 +x = 90 ==> х = 30. Рассматривая прямоугольный треугольник, образованный высотой и гипотенузой, можно заметить, что второй его угол будет равен 90 - x = 60. Это один из углов начального треугольника, значит второй угол будет равен 30 (согласен на словах все слишком каряво, так что стоит все это нарисовать)
ответ: 30; 60
2) угол 120 градусов может быть только углом, против которого лежит основание. Следовательно, углы при основании равны по 30 градусов. В полученном прямоугольном треугольнике основание - гипотенуза, а высота - катет, лежащий против угла в 30 градусов ==> высота = 4/2 = 2
ответ: 2
Дана трапеция ABCD, BC║AD, AB=CD, BC=8см, AD=14см, S(ABCD)=44см².
Найти P(ABCD).
Пусть CM⊥AD, BN⊥AD и M,N∈AD.
Площадь трапеции равна произведению средней линии и высоты опущенной на основание.
S(ABCD) =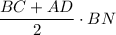 = BN·(8см+14см):2 = BN·11см = 44см²
= BN·(8см+14см):2 = BN·11см = 44см²
BN = 44:11 см = 4см
ΔABN = ΔDCM по гипотенузе и острому углу (AB=DC и ∠BAN=∠CDM т.к. трапеция равнобедренная), поэтому AN=MD
NBCM - прямоугольник, поэтому NM=BC=8см
AN = (AD-NM):2 = (14см-8см):2 = 3см
В прямоугольном ΔABN (∠N=90°): BN=4см и AN=3см, по Египетскому треугольнику AB=5см.
CD=AB=5см
P(ABCD) = AB+BC+CD+AD = 5см+8см+5см+14см = 32см
ответ: 32см.