Проминь od проходить миж сторонами кута aoc видимо до aod=37 cod=53 укажить вид кута aoc

A1. Две прямые на плоскости называются параллельными, если они:

4) не пересекаются

А2. Один из признаков параллельности двух прямых гласит:

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны

А3. Выберите утверждение, являющееся аксиомой параллельных прямых:

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной

А4. Если две параллельные прямые пересечены секущей, то:

Соответственные углы равны

А5. Если прямая перпендикулярна одной из двух параллельных прямых, то:

Она перпендикулярна и другой

А6. Всякая теорема состоит из нескольких частей:

Условия и заключения

А7. При пересечении двух прямых секущей образуются углы, имеющие специальные названия:

Накрест лежащие, соответственные, односторонние

А8. Аксиома – это:

Положение геометрии, не требующее доказательства

А9. Выберите утверждение, которое является признаком параллельности прямых:

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны

А10. Если прямая не пересекает одну из двух параллельных прямых, то:

Другую прямую она тоже не пересекает

или

С другой прямой она совпадает

Можно найти площадь методом нахождения площади всех фигур, при этом прибавив их

Площадь прямоугольника с сторонами 5 и 1 = 5 ед.²

Опустим высоту с стороны прямоугольника длиной 1 ед. Она будет равняться 2, так как высота будет параллельна с высотой слева. У нас получился ещё один прямоугольник с сторонами 5 и 2. Его площадь равна 10 ед.² (если что, для площади прямоугольника мы умножаем стороны)

У нас также появился треугольник с сторонами 2 и (9-5) = 4. Найдём площадь данного треугольника: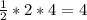 ед.²

Треугольник слева будет равен треугольнику, который мы создали, так что его площади тоже равна 4 ед.²

Прибавляем все значения. Это равняется 23 ед.²