ед.; ед,
Условие данной задачи неполное, а из рисунка напрашивается вывод, что задача на тему "равнобедренные" треугольники ().
=========================================================
Пусть - равнобедренный.
Тогда ед.
Т.к. - медиана ед.
Продлим медиану так, что - середина отрезка .
Также соединим точки , и , .
Получился четырёхугольник .
Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник - параллелограмм.
и - диагонали параллелограмма и они пересекаются.
Точка - пересечение диагоналей и .
Также в : ; : , то есть точкой пересечения делятся пополам.
⇒ - параллелограмм.
⇒ ед., и ед., по свойству параллелограмма.
ед.
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.
⇒ ед.
35°
Объяснение:
По условию BM = DM, а все точки, равноудаленные от концов отрезка BD лежат на серединном перпендикуляре к BD, т.е. на диагонали АС, значит М лежит на АС.
Тогда ∠ВАМ = 45°, а из ΔВАМ
∠АВМ = 180° - (∠АМВ + ∠ВАМ) = 180° - (100° + 45°) = 35°
Из равенства треугольников ВАМ и DKM следует, что
∠KDM = ∠ABM = 35°
По условию АВ = KD, значит
KD = AD = DC.
Тогда ΔADM = ΔKDM по трем сторонам (AD = KD (см. выше), DM - общая, АМ = КМ по условию), значит
∠ADM = ∠KDM = 35°
___
∠KDC = ∠ADC - (∠ADM + ∠KDM) = 90° - (35° + 35°) = 20°
ΔKDC равнобедренный, а значит углы при основании равны:
∠DKC = ∠DCK = (180° - 20°) / 2 = 80°
∠КСМ = ∠DCK - ∠DCA = 80° - 45° = 35°
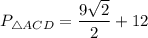 ед.;
ед.; 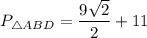 ед,
ед,
Объяснение:Условие данной задачи неполное, а из рисунка напрашивается вывод, что задача на тему "равнобедренные" треугольники (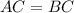 ).
).
=========================================================
Пусть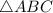 - равнобедренный.
- равнобедренный.
Тогда ед.
ед.
Т.к.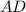 - медиана
- медиана 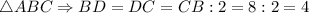 ед.
ед.
Продлим медиану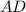 так, что
так, что 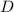 - середина отрезка
- середина отрезка 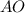 .
.
Также соединим точки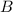 ,
, 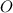 и
и 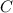 ,
, 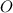 .
.
Получился четырёхугольник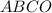 .
.
Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник - параллелограмм.
Точка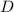 - пересечение диагоналей
- пересечение диагоналей 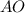 и
и 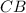 .
.
Также в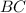 :
: 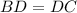 ;
; 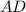 :
: 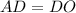 , то есть точкой пересечения делятся пополам.
, то есть точкой пересечения делятся пополам.
⇒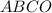 - параллелограмм.
- параллелограмм.
⇒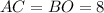 ед., и
ед., и  ед., по свойству параллелограмма.
ед., по свойству параллелограмма.
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.
⇒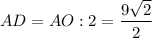 ед.
ед.
35°
Объяснение:
По условию BM = DM, а все точки, равноудаленные от концов отрезка BD лежат на серединном перпендикуляре к BD, т.е. на диагонали АС, значит М лежит на АС.
Тогда ∠ВАМ = 45°, а из ΔВАМ
∠АВМ = 180° - (∠АМВ + ∠ВАМ) = 180° - (100° + 45°) = 35°
Из равенства треугольников ВАМ и DKM следует, что
∠KDM = ∠ABM = 35°
По условию АВ = KD, значит
KD = AD = DC.
Тогда ΔADM = ΔKDM по трем сторонам (AD = KD (см. выше), DM - общая, АМ = КМ по условию), значит
∠ADM = ∠KDM = 35°
___
∠KDC = ∠ADC - (∠ADM + ∠KDM) = 90° - (35° + 35°) = 20°
ΔKDC равнобедренный, а значит углы при основании равны:
∠DKC = ∠DCK = (180° - 20°) / 2 = 80°
∠КСМ = ∠DCK - ∠DCA = 80° - 45° = 35°