S треугольника всегда = высота*основание к которому она проведена разделить это всё на два. (h*осн.)/2
1) высота - 6, основание 12, значит площадь - 12*6/2= 72/2=36 - Б
2)Если в треугольнике есть угол в 30 градусов, то сторона напротив него - в два раза меньше гипотенузы ( стороны напротив прямого=90 угла).
Тут гипотенуза = 12 значит сторона напротив угла равна 12/2 = 6. Чтобы найти вторую сторону используем теорему Пифагора.
a^2+b^2=c^2
где а и б - стороны, а с - гипотенуза. Подставим известное...
6^2+b^2=12^2
36+B^2=144
b^2=144-36
b^2=108
b =
Площадь треугольника здесь - 6*/2 = 3*=18-в
3)Опустим высоту. Найдём её тоже через свойство угла в 30 градусов и теорему пифагора. 16-4=12 значит высота . в итоге.
площадь=*6=6=12 - в
4)Наименьшая высота будет опущена к самой большой стороне, запомни. Опустим ее к стороне 20. Через формулы ( набери в инете среднее геометрическое, долго оформлять очень ) найдём, что x=12,8 - кусочек, которой получается в результате деления высотой стороны двадцать, который ближе к стороне 16. Аналогично найдём и кусочек, ближний к стороне 12. y=7,2. Высота равна корню произведения xy= 9,6 - высота - г
Найдём третью сторону треугольника по теореме косинусов.
Т. косинусов: Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
a²=b²+c²−2⋅b⋅c⋅cosA
a²=8²+ 8²−2⋅8⋅8⋅cos60°
a²=64+64 - 2·8·8·¹/₂
а² = 64
а= 8
2й решения.
2 стороны равны, значит треугольник равнобедренный. Треугольник равнобедренный, значит, углы при основании равны. Углы при основании (180-60)/2 = 60°. Все углы равны, значит, треугольник равносторонний, и третья сторона равна 8 см
S треугольника всегда = высота*основание к которому она проведена разделить это всё на два. (h*осн.)/2
1) высота - 6, основание 12, значит площадь - 12*6/2= 72/2=36 - Б
2)Если в треугольнике есть угол в 30 градусов, то сторона напротив него - в два раза меньше гипотенузы ( стороны напротив прямого=90 угла).
Тут гипотенуза = 12 значит сторона напротив угла равна 12/2 = 6. Чтобы найти вторую сторону используем теорему Пифагора.
a^2+b^2=c^2
где а и б - стороны, а с - гипотенуза. Подставим известное...
6^2+b^2=12^2
36+B^2=144
b^2=144-36
b^2=108
b =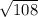
Площадь треугольника здесь - 6*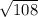 /2 = 3*
/2 = 3*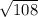 =18
=18 -в
-в
3)Опустим высоту. Найдём её тоже через свойство угла в 30 градусов и теорему пифагора. 16-4=12 значит высота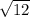 . в итоге.
. в итоге.
площадь=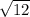 *6=6
*6=6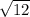 =12
=12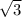 - в
- в
4)Наименьшая высота будет опущена к самой большой стороне, запомни. Опустим ее к стороне 20. Через формулы ( набери в инете среднее геометрическое, долго оформлять очень ) найдём, что x=12,8 - кусочек, которой получается в результате деления высотой стороны двадцать, который ближе к стороне 16. Аналогично найдём и кусочек, ближний к стороне 12. y=7,2. Высота равна корню произведения xy= 9,6 - высота - г
8см
Объяснение:
1й решения.
Найдём третью сторону треугольника по теореме косинусов.
Т. косинусов: Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
a²=b²+c²−2⋅b⋅c⋅cosA
a²=8²+ 8²−2⋅8⋅8⋅cos60°
a²=64+64 - 2·8·8·¹/₂
а² = 64
а= 8
2й решения.
2 стороны равны, значит треугольник равнобедренный. Треугольник равнобедренный, значит, углы при основании равны. Углы при основании (180-60)/2 = 60°. Все углы равны, значит, треугольник равносторонний, и третья сторона равна 8 см