По стороне основания а и боковому ребру b найдите полную поверхность правильной призмы: 1) треугольной; 2) четырехугольной

Показать ответ

Ответ:

slavaglybochka

02.11.2021 05:07

Проведем МК параллельно основанию трапеции, тогда это средняя линия трапеции. Также она делит сторону треугольника пополам, значит это медиана. Медиана треугольника делит его на 2 треуг. с одинаковыми площадями, значит площадь треугольника МСК=12 и площадь МКД=12. Что такое площадь? ЭТо половина произведения основания на высоту треугольника. к примеру основание МК и высота СН или основание МК и высота ДН1 для МСК и МКД соответственно. их площади равны 12, значит 12=0,5 МК*СН к примеру, 24=МК*СН. это площадь треугольника. а площадь трапеции равна произведению средней линии на высоту, т е МК-средняя линия, а СН половина высоты, значит 24 в выражении еще умножим на 2,т к в выражении лишь половина высоты, итого площадь трапеции =48

0,0(0 оценок)

Ответ:

vladpin01

12.10.2022 21:30

Дано:

Правильная четырёхугольная пирамида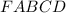 FABCD .

AB=6 (см).

FG=10 (см).

Найти:

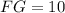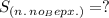$S_{(n. \: no_Bepx.)}=?$ (см²).

Решение:

$\boxed{S_{(n. \: no_Bepx.)}=S_{(oc_Ho_B.)}+S_{(6o_K. \: no_Bepx.)}}$

Значит сначала мы должны найти площадь основания пирамиды, а затем площадь боковой поверхности пирамиды.

В основании правильной четырёхугольной пирамиды лежит квадрат, поэтому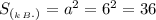 $S_{(_k_B.)}=a^2=6^2=36$ (см²).

Площадь боковой поверхности правильной четырёхугольной пирамиды - полупроизведение периметра основания на апофему.

Значит нам нужно сначала найти апофему нашей пирамиды.

1 правило: Апофема делит сторону основания пополам.2 правило: Катет прямоугольного треугольника, который образован апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной четырехугольной пирамиды.

Объяснение 1 правила: из этого следует, что апофема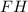 делит сторону основания 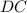так, что 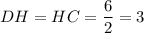$DH=HC=\dfrac{6}{2}=3$ (см).

Объяснение 2 правила: внутри нашей пирамиды образовался прямоугольный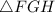 $\triangle FGH$ , где 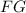- катет прямоугольного тр-ка (высота пирамиды); 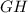- катет прямоугольного тр-ка; 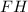- гипотенуза прямоугольного тр-ка (апофема пирамиды). По данному правилу можно сказать, что 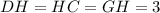DH=HC=GH=3 (см).

Так как апофема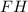 нашей пирамиды является ещё и гипотенузы прямоугольного 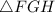$\triangle FGH$ , то мы сможем найти её величину по т.Пифагора:

$FH=\sqrt{FG^2+GH^2}=\sqrt{10^2+3^2}=\sqrt{100+9}=\sqrt{109}$ (см).

Теперь найдём периметр основания (квадрата):

$P=4a=6\cdot4=24$ (см).

Затем найдём площадь боковой поверхности:

$S_{(6ok. \: no_B.)} =P_{(oc_Ho_B.)}\cdot\dfrac{1}{2}\cdot FH=24\cdot\dfrac{1}{2}\cdot\sqrt{109}=12\sqrt{109}$ (см²).

Остаётся найти ответ на вопрос: "Чему равна площадь полной поверхности пирамиды?"

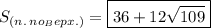$S_{(n. \: no_Bepx.)}=\boxed{36+12\sqrt{109}}$ (см²).

ответ: $\boxed{S_{(n. \: no_Bepx.)}=36+12\sqrt{109}}$ (см²).
Найти полную поверхность правильной четырехугольной пирамиды, сторона основания которой 6 см, а высо