по геометрий соч уже 7 раз

Найти периметр трапеции по готовому чертежу

Объяснение:

∠BCО = ∠ОЕА= 30°  как накрест лежащие , при секущей СЕ.

По т. о внешнем угле треугольника в ΔЕАО ,  ∠ЕОА=60°-30°=30°. Откуда ∠AOE = ∠BOC = 30° ⇒ ∠ВОС=30°.

Значит ΔЕАО=ΔСВО по стороне и 2-м прилежащим углам:

        ОА=ОВ по условию,

        ∠AOE = ∠BOC = 30°  ,

         ∠ЕАО=∠СВО как накрест лежащие ,АВ-секущая.

В равных треугольниках соответственные элементы равны ⇒ЕА=ВС.

Пусть ЕА=ВС=а. Т.к. ΔЕАО , ΔСВО-равнобедренные , то ЕА=ОА=ВС=ОВ=а . Тогда сторона трапеции АВ=2а ⇒ СD=2а (*),

т.к АВСD-равнобедренная трапеция( ∠D=180°-120°=60°)

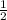Из Δ ECD -прямоугольный , ЕD=ЕА+АD=а+15 найдем  CD = ED = (**).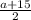

Приравняем полученные выражения (*) и (**) , получим

2а =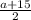  , 4а=а+15 , а=5 ⇒ ВС=5, АВ=СD=10

P(ABCD) = 5 + 15 +2* 10 =40 .

ABCD - параллелограмм

\begin{gathered}\overrightarrow{AD} = \overrightarrow a \\ \\ \overrightarrow{AB} = \overrightarrow b \\ \\ K \in BC, ~L \in ADBK:KC=3:4, ~AL:LD=4:3\end{gathered}

AD

=

a

AB

=

b

K∈BC, L∈AD

BK:KC=3:4, AL:LD=4:3

Выразить вектор \overrightarrow {KL}

KL

через вектора \overrightarrow a, ~\overrightarrow b

a

,

b

\displaystyle \overrightarrow{KL} =\overrightarrow{KB} +\overrightarrow{BA}+ \overrightarrow {AL}

KL

=

KB

+

BA

+

AL

(по правилу суммы нескольких векторов)

Рассмотрим параллелограмм ABCD

AD = BC по свойству параллелограмма

AD ║ BC - по определению параллелограмма

\Rightarrow \overrightarrow{BC} = \overrightarrow{AD} = \overrightarrow a⇒

BC

=

AD

=

a

\begin{gathered}\displaystyle \overrightarrow {KB} = \frac{3}{7}\overrightarrow{CB} = -\frac{3}{7}\overrightarrow{BC} = -\frac{3}{7}\overrightarrow a \\ \\ \overrightarrow {BA} = -\overrightarrow {AB} = -\overrightarrow b \\ \\ \overrightarrow {AL} = \frac{4}{7}\overrightarrow{AD} = \frac{4}{7}\overrightarrow{a}\end{gathered}

KB

=

7

3

CB

=−

7

3

BC

=−

7

3

a

BA

=−

AB

=−

b

AL

=

7

4

AD

=

7

4

a

\displaystyle \overrightarrow{KL} =\overrightarrow{KB} +\overrightarrow{BA}+ \overrightarrow {AL} = -\frac 3 7 \overrightarrow a - \overrightarrow b + \frac 4 7 \overrightarrow a = \frac 1 7 \overrightarrow a - \overrightarrow b

KL

=

KB

+

BA

+

AL

=−

7

3

a

−

b

+

7

4

a

=

7

1

a

−

b

\displaystyle \text{Answer}: \boxed{\overrightarrow {KL} = \frac 1 7 \overrightarrow a - \overrightarrow b}Answer:

KL

=

7

1

a

−

b