Катет АС противолежит углу 30° и равен половине гипотенузы АВ.
АС=5 см.
Окружность и прямая могут касаться и иметь одну общую точку, не касаться и не иметь общих точек, или пересекаться, при этом они будут иметь две общие точки .
1) радиус, проведенный в точку касания, равен катету r=АС =5 см( т.к. угол ВСА=90°, а радиус перпендикулярен касательной в точке касания)
2) Окружность не будет касаться прямой ВС, если её радиус меньше катета АС. r < AC; r < 5 см
3) Окружность и прямая пересекутся, если радиус больше расстояния от центра окружности до прямой. r > AC' r > 5 см
5
Объяснение:
Катет АС противолежит углу 30° и равен половине гипотенузы АВ.
АС=5 см.
Окружность и прямая могут касаться и иметь одну общую точку, не касаться и не иметь общих точек, или пересекаться, при этом они будут иметь две общие точки .
1) радиус, проведенный в точку касания, равен катету r=АС =5 см( т.к. угол ВСА=90°, а радиус перпендикулярен касательной в точке касания)
2) Окружность не будет касаться прямой ВС, если её радиус меньше катета АС. r < AC; r < 5 см
3) Окружность и прямая пересекутся, если радиус больше расстояния от центра окружности до прямой. r > AC' r > 5 см
Объяснение:
1. A(0;0) B(9;10).
Уравнение прямой:
ответ: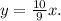
2. A(0;0) B(5;0) C(12;-3) Dₓ=?
ответ: Dₓ=7.
3. M(2;-4) K(3,5) P(x;y)=?
ответ: P(-1;-31).
4.
(x-3)²+(y-5)²=49
(x-3)²+(y-5)²=7²
Графиком этого уравнения является окружность, центр которой смещён вправо вдоль оси Ох на 3 единицы и опущен вниз вдоль
оси Оу на 5 единиц с радиусом 7 единиц.
Рассиояние от центра окружности (x-3)²+(y-5)²=7² до прямой х=-2
равно: 3-(-2)=3+2=5<R(7) ⇒ Прямая пересекает окружность в двух точках.
5. Рассмотрим ΔАКО. АК=КО=АО*tg∠АОК=8*√2*√2/2=8 (cм).
Рассмотрим ΔВСО. ОС=√(ОВ²-ВС²)=√(10²-8²)=√(100-64)=√36=6 (см).
Продлим прямые АК и ВС до точки пересечения F. ⇒
AF=8+6=14 (см) BF=4528+8=16 (см).
AB=√(AF²+BF²)=√(14²+16²)=√(196+256)=√452=2√113≈21,26 (см).
A(-8;-8) B(8;-6).