Плоскость альфа пересекает стороны KM и KN треугольника KMN в точках P и E соответственно. КР: PM=KE:EN = 3:2. а) Докажите, что MN || альфа b) Известно, что PE = 6 Найдите MN.
Объяснение: что бы найти координаты точки пересечения диагоналей надо знать что при пересечении он делят друг друга пополам тогда нам нужно всего лишь знать координаты вершин B и D они нам известны и также есть формула середины координат отрезка вычислим тогда получим координаты середины отрезка BD будут (-1/2 ; 2) теперь найдем координаты вершины С так если вычислять середину отрезка AC то координаты будут точно такими же как и у отрезка BD пусть координаты середины отрезка AC(x;y) найдем середину тогда x=-3 а y=-5 то есть С(-3;-5)
ответ: координаты вершины С(-3;-5) ; точка пересечения диагоналей (-1/2 ; 2)
Объяснение: что бы найти координаты точки пересечения диагоналей надо знать что при пересечении он делят друг друга пополам тогда нам нужно всего лишь знать координаты вершин B и D они нам известны и также есть формула середины координат отрезка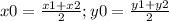
вычислим 
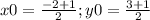тогда получим координаты середины отрезка BD будут (-1/2 ; 2) теперь найдем координаты вершины С так если вычислять середину отрезка AC то координаты будут точно такими же как и у отрезка BD пусть координаты середины отрезка AC(x;y) найдем середину 
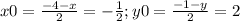тогда x=-3 а y=-5 то есть С(-3;-5)
<Х=118°
Объяснение:
∆ABD- прямоугольный треугольник, т.к. <АВD вписанный угол опирается на дугуАD=180°
Сумма острых углов в прямоугольном треугольнике равна 90°
<DAB+<BDA=90°
<DAB=90°-<BDA=90°-28°=62°
<DAB- вписанный угол опирается на дугуВD(меньшая)
Тогда дугаВD(меньшая)=2*<DAB=2*62°=124°
Вся окружность составляет полный угол который равен 360°
дугаВD(меньшая)+дугаВD(боль)=360°
ДугаВD(боль)=360°-дугаВD(меньшая)=
=360°-124°=236°
<ВСD- вписанный угол опирается на дугуВD(боль)
<ВCD=дугаВD(боль):2=236°:2=118°
Обозначение:
дугаВD(боль)- большая дугаBD