(2x+2y =22
(x^2+y^2=10.5^2
(x+y=11
(x^2+y^2=110.25
отв :20
Объяснение:
Периметр прямоугольника определяеся по формуле
, где a,b - стороны прямоугольника .
Если Р = 22ед., то сумма двух соседних сторон сторон равна полупериметру, то есть 11 ед.
Пусть одна сторона прямоугольника будетx ед. Тогда (11- x ) ед.- другая сторона . Площадь прямоугольника определяется по формуле
, a и b стороны. Составим и решим уравнение:
Если одна сторона ед , то другая ед.
Если одна сторона ед, то другая ед.
Значит стороны прямоугольника ед. и ед.
Диагональ прямоугольника найдем по теореме Пифагора : квадрат гипотенузы равен сумме квадратов катетов .
d= 10 ед.
Периметр прямоугольника:
Р = 2 * (а + b) = 22 ⇒ a + b = 11
Площадь прямоугольника:
S = a * b = 10,5
Рассмотрим закрашенный прямоугольный треугольник:
По теореме Пифагора a² + b² = c²
Воспользуемся формулой квадрата суммы двух переменных:
(a + b)² = a² + 2*a*b + b²
11² = a² + 2*10,5 + b²
121 = a² + 21 + b²
a² + b² = 100
c² = 100 ⇒ c = ± 10 ⇒ c = 10 е.д. - диагональ прямоугольника
ответ: 10.
(2x+2y =22
(x^2+y^2=10.5^2
(x+y=11
(x^2+y^2=110.25
отв :20
Объяснение:
Периметр прямоугольника определяеся по формуле
Если Р = 22ед., то сумма двух соседних сторон сторон равна полупериметру, то есть 11 ед.
Пусть одна сторона прямоугольника будетx ед. Тогда (11- x ) ед.- другая сторона . Площадь прямоугольника определяется по формуле
Если одна сторона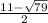 ед , то другая
ед , то другая 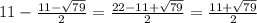 ед.
ед.
Если одна сторона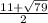 ед, то другая
ед, то другая 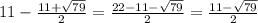 ед.
ед.
Значит стороны прямоугольника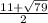 ед. и
ед. и 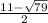 ед.
ед.
Диагональ прямоугольника найдем по теореме Пифагора : квадрат гипотенузы равен сумме квадратов катетов .
d= 10 ед.
Периметр прямоугольника:
Р = 2 * (а + b) = 22 ⇒ a + b = 11
Площадь прямоугольника:
S = a * b = 10,5
Рассмотрим закрашенный прямоугольный треугольник:
По теореме Пифагора a² + b² = c²
Воспользуемся формулой квадрата суммы двух переменных:
(a + b)² = a² + 2*a*b + b²
11² = a² + 2*10,5 + b²
121 = a² + 21 + b²
a² + b² = 100
c² = 100 ⇒ c = ± 10 ⇒ c = 10 е.д. - диагональ прямоугольника
ответ: 10.