Пусть ВС = a, AD = b, и пусть h – высота трапеции (см. рисунок)
По свойству (диагонали трапеции разбивают её на четыре треугольника с общей вершиной, площади треугольников, прилежащих к боковым сторонам, равны.) S(ABO)=S(CDO) , обозначим эту площадь S0 (действительно, S (ABD) = S(ACD) , т. к. у них общие основания и равные высоты, т. е. S(AOB)+S(AOD)=S(COD)+S(AOD) откуда следует S(AOB) =S(COD)).
Так как S(ABC)= S0+ S1= h*a/2 и S(ACD)= S0+ S2= h*b/2 , то (S0+S1)/(S0+S2)=a/b
Далее, треугольники BOC и DOA подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит S1/S2=(a/b)^2
Таким образом, (S0+S1)/(S0+S2) =
Отсюда находим S1= =36/9=4
Поэтому площадь трапеции будет равна s= S1+S2+2S0= 4+9+12=25
Сумма углов треугольника = 180 °. У равнобедренного треугольника углы при основании равны.
1 вариант. Угол при вершине в 4 раза больше угла при основании.Тогда:
Каждый угол при основании - х ° Угол при вершине - 4х° х+х+4х= 180 6х=180 х=180 :6 х= 30° - каждый угол при основании 4×30°= 120 ° - угол при вершине Это будет тупоугольный треугольник. ответ: 30°,30°, 120°.
2 вариант. Угол при основании в 4 раза больше, чем угол при вершине треугольника. Угол при вершине - х ° Каждый угол при основании - 4х° 4х+4х+х= 180 9х=180 х=180 :9 х= 20° - угол при вершине 20×4 = 80° - каждый угол при основании треугольника. Это остроугольный треугольник. ответ: 20°, 80°, 80°.
По свойству (диагонали трапеции разбивают её на четыре треугольника с общей вершиной, площади треугольников, прилежащих к боковым сторонам, равны.) S(ABO)=S(CDO) , обозначим эту площадь S0 (действительно, S (ABD) = S(ACD) , т. к. у них общие основания и равные высоты, т. е. S(AOB)+S(AOD)=S(COD)+S(AOD) откуда следует S(AOB) =S(COD)).
Так как S(ABC)= S0+ S1= h*a/2 и S(ACD)= S0+ S2= h*b/2 , то (S0+S1)/(S0+S2)=a/b
Далее, треугольники BOC и DOA подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит S1/S2=(a/b)^2
Таким образом, (S0+S1)/(S0+S2) =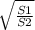
Отсюда находим S1= =36/9=4
=36/9=4
Поэтому площадь трапеции будет равна s= S1+S2+2S0= 4+9+12=25
У равнобедренного треугольника углы при основании равны.
1 вариант.
Угол при вершине в 4 раза больше угла при основании.Тогда:
Каждый угол при основании - х °
Угол при вершине - 4х°
х+х+4х= 180
6х=180
х=180 :6
х= 30° - каждый угол при основании
4×30°= 120 ° - угол при вершине
Это будет тупоугольный треугольник.
ответ: 30°,30°, 120°.
2 вариант.
Угол при основании в 4 раза больше, чем угол при вершине треугольника.
Угол при вершине - х °
Каждый угол при основании - 4х°
4х+4х+х= 180
9х=180
х=180 :9
х= 20° - угол при вершине
20×4 = 80° - каждый угол при основании треугольника.
Это остроугольный треугольник.
ответ: 20°, 80°, 80°.