Перед посівом соняшників у підприємців виникло питання щодо вибору найбільш врожайного сорту .Один з багатьох запропонованих сортів дає можливість виростити соняшники діаметром 30 см (у середньому)а другий -соняшники діаметром 20 см (у середньому).При цьому числьність на 1 га рослин першого сорту вдвічі менша від чисельності на 1 га рослин другого сорту.Який сорт вибрали підприємці?

Пусть дан △АВС равнобедренный , ВС - основание, т.О ∈ ВС, F ∈ AB,

E ∈ AC ; ОЕ || АВ и ОF || АС ; ОFАЕ = 32см. Найдём АВ - ?

                                                        Решение

∠1 = ∠2 потому что △ АВС равнобедренный ( по условию ).

ОF || АС по условию, поэтому ∠2  =∠3 ( соответственные углы образованные при пересечении этих прямых секущей ВО ), значит

∠1 =∠3.

Рассмотрим △ВFO : равнобедренный, BF = FO.

ОЕ || АВ и ОF || АС по условию,значит OFAE - параллелограмм.

По свойству сторон и углов параллелограмма AF = OE и FO = AE.

Найдём периметр РОFАЕ :

Р(ОFАЕ) = 2 * AF + 2 * FO

Р(ОFАЕ) = 2( AF+FO)

BF = FO , то Р(ОFАЕ) = 2( AF + BF)

Р(ОFАЕ) = 2 * АВ

АВ =  Р(ОFАЕ) /2 = 32/2 = 16

а) (-2;0) - центр окружности, радиус окружности равен 3.

б) (0; 4) - центр окружности, радиус окружности равен .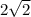

в) (5; -7) - центр окружности, радиус окружности равен 4.

Объяснение:

Уравнение окружности имеет вид: (x-a)²+(y-b)²=R². Здесь центр окружности (a; b) . R - радиус окружности.

а) (-2; 0) -центр окружности, R²=9. R²=3². R=3.

б) (0; 4) - центр окружности, ,  .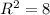

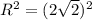
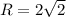в) (5; -7) - центр окружности, R²=16,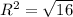 ,  R=4.

Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень