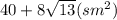расстояние от K до ABC (обозначим KO) - это перпендикуляр к ABC => из прямоугольного треугольника KOA по т.Пифагора KO = корень(AK^2-AO^2). AK=10 по условию.
Точка O - центр треугольника ABC, она лежит на высоте(медиане и биссектрисе) AN и делит AN в отношении 2:1 AO=2*ON
из прямоугольного треугольника ABN AN = корень(AB^2-BN^2). AB=15 по условию, BN=15/2 (т.к. AN высота и медиана правильного треугольника) AN = корень(15*15-15*15/4) = корень(3*15*15/4) = 15/2*корень(3)
ON = AN/3 = 5/2*корень(3)
AO = 2*ON = 5*корень(3)
KO = корень(10*10-5*5*3) = корень(100-75) = корень(25) = 5
расстояние от K до ABC (обозначим KO) - это перпендикуляр к ABC => из прямоугольного треугольника KOA по т.Пифагора KO = корень(AK^2-AO^2). AK=10 по условию.
Точка O - центр треугольника ABC, она лежит на высоте(медиане и биссектрисе) AN и делит AN в отношении 2:1 AO=2*ON
из прямоугольного треугольника ABN AN = корень(AB^2-BN^2). AB=15 по условию, BN=15/2 (т.к. AN высота и медиана правильного треугольника) AN = корень(15*15-15*15/4) = корень(3*15*15/4) = 15/2*корень(3)
ON = AN/3 = 5/2*корень(3)
AO = 2*ON = 5*корень(3)
KO = корень(10*10-5*5*3) = корень(100-75) = корень(25) = 5
Объем призмы - это произведение площади её основания на высоту
Площадь боковой поверхности призмы - это произведение периметра основания на длину бокового ребра.
Так как призма прямая, то высота равна длине боковой грани.
А значит площадь основания:
В основании призмы прямоугольный треугольник. Его площадь можно найти по формуле
Так как катеты соотносятся как 2 и 3, то введём коэффициент пропорциональности k:
a=2k;
b=3k;
Значит а=2*2=4 (см), а b= 3*2=6 (cм).
Площадь боковой поверхности прямой призмы находится по формуле :
Где P - это периметр основания.
Для нахождения периметра нам не хватает гипотенузы. Найдём её по теореме Пифагора:
Площадь боковой поверхности:
S=10*4+2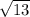 *4=40+8
*4=40+8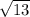 см2.
см2.
ответ: