Отрезок DM - биссектриса треугольника CDE. Через точку M проведена прямая, параллельная стороне DE и пересекающая сторону DC в точке N найти треугольник DMN, если CDE = 59о
B C Если сторона AD больше каждой соседней стороны (в данном случае AB и CD) на 2 см, это значит, что стороны AB и CD на 2 см меньше стороны AD. Если сторона AD на 4 см меньше противолежащей стороны BC, это значит, что сторона BC на 4 см больше стороны AD. 1) 12-2=10 (см) - стороны AB, CD. 2) 12+4=16 (см) - сторона BC. Сумма длин всех сторон - это периметр, то есть складываем все 4 стороны: 3) 12+10+10+16=48 (см) - периметр. ответ: 48 см.
Тт. и лежат в одной плоскости и, будучи соединены последовательно, образуют равнобокую трапецию ( — средняя линия поэтому ).
Поэтому угол, о котором идет речь в условии задачи — это угол между диагоналями трапеции.
Далее возможны два варианта: либо тогда (см. рис. 2).
Решим задачу в общем виде (рис. 3). Пускай Продлим нижнее основание за точку на длину верхнего основания: Тогда образовавшийся четырехугольник — параллелограмм, Значит а
По теореме синусов
используя формулу приведения и формулу синуса двойного угла найдем длину диагонали:
Треугольники и подобны, значит и отсюда
По теореме косинусов для треугольника
откуда
Тогда если
Если же тогда
Теперь возвращаясь к призме, можем вычислить ее высоту. В прямоугольном треугольнике по теореме Пифагора:
если
если
(при таком значении угла не складывается пространственная фигура — ее высота равна 0, следовательно, случай — посторонний).
Площадь основания призмы вычислим по формуле площади равностороннего треугольника
A D
B C
Если сторона AD больше каждой соседней стороны (в данном случае AB и CD) на 2 см, это значит, что стороны AB и CD на 2 см меньше стороны AD.
Если сторона AD на 4 см меньше противолежащей стороны BC, это значит, что сторона BC на 4 см больше стороны AD.
1) 12-2=10 (см) - стороны AB, CD.
2) 12+4=16 (см) - сторона BC.
Сумма длин всех сторон - это периметр, то есть складываем все 4 стороны:
3) 12+10+10+16=48 (см) - периметр.
ответ: 48 см.
Объем призмы равен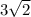
Объяснение:
(Рис. 1)
Тт.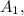
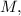
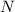 и
и 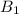 лежат в одной плоскости и, будучи соединены последовательно, образуют равнобокую трапецию (
лежат в одной плоскости и, будучи соединены последовательно, образуют равнобокую трапецию (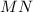 — средняя линия
— средняя линия 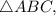 поэтому
поэтому 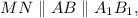
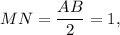
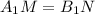 ).
).
Поэтому угол, о котором идет речь в условии задачи — это угол между диагоналями трапеции.
Далее возможны два варианта: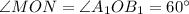 либо
либо 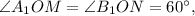 тогда
тогда 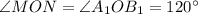 (см. рис. 2).
(см. рис. 2).
Решим задачу в общем виде (рис. 3). Пускай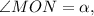
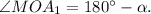 Продлим нижнее основание
Продлим нижнее основание 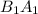 за точку
за точку 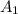 на длину верхнего основания:
на длину верхнего основания: 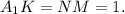 Тогда образовавшийся четырехугольник
Тогда образовавшийся четырехугольник 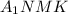 — параллелограмм,
— параллелограмм, 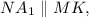
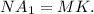 Значит
Значит 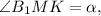 а
а
По теореме синусов
используя формулу приведения и формулу синуса двойного угла найдем длину диагонали:
Треугольники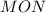 и
и 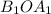 подобны,
подобны, 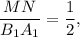 значит и
значит и 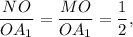 отсюда
отсюда
По теореме косинусов для треугольника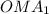
откуда
Тогда если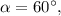
Если же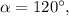 тогда
тогда
Теперь возвращаясь к призме, можем вычислить ее высоту. В прямоугольном треугольнике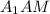 по теореме Пифагора:
по теореме Пифагора:
если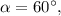
если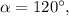
(при таком значении угла не складывается пространственная фигура — ее высота равна 0, следовательно, случай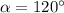 — посторонний).
— посторонний).
Площадь основания призмы вычислим по формуле площади равностороннего треугольника
Окончательно, объем призмы: