отрезки AB и CD пересекаются в их общей середине O. На отрезке AC и BD отмечены точки K и K¹ так что AK=BK¹. Докажите что а) OK=OK¹;б) точка O лежит на прямой KK¹

ответ: S2 уменьшилась на 43,75% ; V2 уменьшился на 57,875% Объяснение:

25%=25/100=1/4 - на столько уменьшится каждая сторона и станет 1-1/4=3/4 от исходной.

При уменьшении всех сторон параллелепипеда уменьшаются и все  его линейные размеры, т.е.  высота самого параллелепипеда и его сторон. Получится фигура, подобная исходной с коэффициентом подобия k=3/4:1=3/4.

  Отношение площадей подобных фигур  равно квадрату коэффициента их подобия.

Примем площадь исходной фигуры  равной Ѕ1, а площадь уменьшенной фигуры Ѕ2.

Тогда Ѕ2:Ѕ1=k^2=(3/4)^2=9/16

S2-S1=16/16-9/16=7/16 ( на столько уменьшилась площадь поверхности)

В процентном выражении это будет 7•100/16=43,75%

  Отношение объемов подобных фигур равно кубу коэффициента их подобия:

   Если объем исходной фигуры V1 и уменьшенной V2, то V2:V1=k^3=27/64 =>

V1-V2=64/64-27/64=37/64 ( на столько уменьшился объем.

В процентном выражении это 37•100:64=57,875%

<2 в два раза больше <1

Объяснение:

1) Т.к. вершина <1 лежит на окружности, а его стороны пересекают окружность, то <1 - вписанный и равен половине дуги на которую опирается.

<1 опирается на дугу AC (по чертежу), следовательно ∪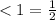

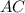
2) Вершина <2 лежит в центре окружности, а стороны угла - радиусы окружности, следовательно <2 - центральный. Известно, что центральный угол равен величине дуги на которую опирается. По чертежу видно, что <2 опирается на дугу AC, т.е ∪ .

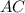3) <1 равен половине дуги AC, а <2 равен целой дуге AC, следовательно  <2 в 2 раза больше <1