Отметьте точки а и в не лежащие на прямой с. отметьте точки m и n лежащие на прямой а. проведите прямую проходящую через точки m и n.

2.даны вертикальные углы авс и dвс. угол авс равен 450. найдите угол dвс.

3. периметр равнобедренного треугольника равен 23 м. найдите его стороны, если основание меньше боковой стороны на 4 см.

4. на биссектрисе угла а взята точка в, а на сторонах угла — точки с и d, такие, что угол abcравен углу abd. докажите, что ad = ас.

5.на основании ас равнобедренного треугольника abc отмечены точки м и к так, что угол abm равен углу cbk.. докажите, что треугольник авм равен треугольнику свк

Показать ответ

Ответ:

Nurik271100

09.12.2021 11:34

ответ: 2

Объяснение:

$\displaystyle S_{n.n}=2S_{osn} +4S_{bok}$ , где

Sп.п - площадь полной поверхности

Sосн. - площадь основания

Sбок - площадь боковой грани

Рассмотрим основание призмы

Мы можем узнать сторону основания(понадобиться позже). Тк. по свойству ромба его диагонали перпендикулярны и делятся пополам, то ромб разбит на 4 равных прямоугольных треугольника с катетами 5 и 12. Рассмотрим 1 из них.

По т. Пифагора:

$\displaystyle a=\sqrt{5^2+12^2}=\sqrt{25+144}=\sqrt{169}=13$

Площадь ромба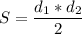 $\displaystyle S = \frac{d_{1}* d_{2}}{2}$

$\displaystyle S = \frac{10*24}{2} =120$

Подставляем в формулу площади полной поверхности призмы

$\displaystyle 344=2*120+4S_{bok}$

$\displaystyle 4S_{bok}=344-240$

$\displaystyle 4S_{bok}=104$

$\displaystyle S_{bok}=26$

Мы знаем, что боковая грань - прямоугольник,т.е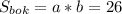 $\displaystyle S_{bok}=a*b=26$

Т.к. нам известна одна из сторон(сторона основания, которая равна 13), то мы можем найти и боковое ребро

$\displaystyle b=26:13 = 2$

В основании прямой призмы лежит ромб с диагоналями, равными 10 и 24. Площадь ее поверхности равна 34

0,0(0 оценок)

Ответ:

малина106

11.10.2022 04:14

в) и д)

Объяснение:

Определение: углом между наклонной и плоскостью называется острый угол между наклонной и ее проекцией на эту плоскость.

Угол α между наклонной, опущенной из точки Т в плоскость ψ, верно обозначен на рисунках в) и д), так как на данных рисунках из точки Т опущен перпендикуляр к ОМ, лежащей в плоскости ψ, и из той же точки Т проведена наклонная, основание которой принадлежит ОМ.

Следовательно, ОМ является проекцией наклонной ТМ на плоскость ψ, а угол α - это угол между наклонной ТМ и её проекцией МО на плоскость ψ.

ответ: в) и д)

0,0(0 оценок)

Популярные вопросы: Геометрия