Если у прямоугольных треугольников равен острый угол, то это значит, что тангенс этого угла будет одинаковый у обоих треугольников. Тангенс - это отношение противолежащего катета к прилежащему. Значит,
- равный угол, а и b - катеты. Из выражения видим, что если тангенс и один из катетов у треугольников равны, то и второй катет у них тоже будет равным. Если у прямоугольных треуцгольников равны 2 катета, то корень и суммы их квадратов(это их гипотенуза) у них тоже будет равным. Или же они равны по двум катетам и углу между ними.
6. <ACE - внешний для угла <ACB => <ACE=<ABC+<BAC, и углы <ABC и <BAC равны по условию.
При этом <ACE=<ACD+<ECD и <ACD и <ECD также равны между собой по условию. Значит <BAC=<ACD - а это накрест лежащие углы при прямых AB и CD и секущей АС. => AB || CD чтд.
Что и требовалось доказать
Объяснение:
Если у прямоугольных треугольников равен острый угол, то это значит, что тангенс этого угла будет одинаковый у обоих треугольников. Тангенс - это отношение противолежащего катета к прилежащему. Значит,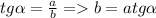
Объяснение:
5. Есть в принципе теорема, что сумма внешних углов равно 360°. Но можно для этой задачи расписать:
α=<B+<C; β=<A+<C; γ=<A+<B - по теореме "Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с этим внешним углом."
Получается α+β+γ=<B+<C+<A+<C+<A+<B=2*(<A+<B+<C)=2*180=360°
6. <ACE - внешний для угла <ACB => <ACE=<ABC+<BAC, и углы <ABC и <BAC равны по условию.
При этом <ACE=<ACD+<ECD и <ACD и <ECD также равны между собой по условию. Значит <BAC=<ACD - а это накрест лежащие углы при прямых AB и CD и секущей АС. => AB || CD чтд.